W przypadku małych oscylacji proste wahadło zachowuje się liniowo, co oznacza, że jego ruch można opisać równaniem liniowym, ale przy większych amplitudach staje się ono bardzo nieliniowe, z zależnością sinusoidalną w równaniu ruchu.
Problemy
Spróbuj użyć wykresu i zmienić parametry, takie jak masa, długość, grawitacja, aby odpowiedzieć na te pytania (ustaw tłumienie na zero, aby uprościć problem):
- Jaki jest związek między przyspieszeniem kątowym a kątem?
- Jak masa, długość oraz przyspieszenie grawitacyjne wpływa na zależność między przyspieszeniem kątowym a kątem?
- Jak długość oraz przyspieszenie grawitacyjne, w przypadku małych oscylacji, wpływa na okres lub częstotliwość oscylacji?
Znajdziesz odpowiedzi poniżej.
Zależności fizyczne - ruch obrotowy bryły sztywnej
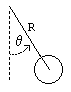
zmienne wahadła
Wahadło jest modelowane jako masa punktowa na końcu bezmasowego pręta. Definiujemy następujące zmienne:
- θ = kąt wahadła ( 0= pion)
- R = długość pręta
- T = naprężenie pręta
- m = masa wahadła
- g = przyspieszenie grawitacyjne
Wyprowadzimy równanie ruchu wahadła korzystając z drugiej zasady dynamiki, ruchu obrotowego bryły sztywnej wokół ustalonej osi, która ma postać τ = I α gdzie
- τ = wypadkowy moment siły
- I = moment bezwładności
- α = θ''= przyspieszenie kątowe
Moment bezwładności dla danej osi obrotu to I = m R2 . Moment siły można obliczyć jako iloczyn wektorowy wektora położenia i siły. Wartość momentu siły grawitacji okazuje się być równa τ = −R m g sin θ . Tak więc mamy
−R m g sin θ = m R2 α
co upraszcza się do
| θ'' = − g⁄R sin θ | (1) |
Jest to równanie ruchu wahadła.
Zależności fizyczne - ruch punktu materialnego
Większość ludzi jest mniej zaznajomiona z momentem bezwładności i momentem obrotowym niż z prostą masą i przyspieszeniem występującymi w drugiej zasadzie dynamiki Newtona, F = m a . Aby pokazać, że nie ma nic nowego w tej szczególnej wersji drugiej zasady Newtona dla ruchu obrotowego, wyprowadzamy tutaj równanie ruchu bez dynamiki ruchu obrotowego. Jak zobaczysz, ta metoda jest nieco bardziej skomplikowana algebraicznie.
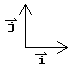
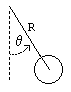
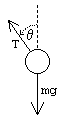
siły działające na wahadło
Potrzebujemy standardowych wektorów jednostkowych, i, j . Do oznaczenia wektora używamy pogrubienia i kreski nad symbolem.
- i = wektor jednostkowy w kierunku poziomym
- j = wektor jednostkowy w kierunku pionowym
Opis kinematyczny ruchu wahadła jest wtedy następujący
położenie = R sin θ i − R cos θ j
prędkość = R θ' cos θ i + R θ' sin θ j
przyspieszenie = R(θ'' cos θ i − θ' 2 sin θ i + θ'' sin θ j + θ' 2 cos θ j)
Położenie uzyskuje się dzięki prostym zależnościom trygonometrycznym. Następnie prędkość i przyspieszenie liczymy jako pierwszą i drugą pochodną położenia.
Dalej rysujemy diagram sił dla wahadła. Siły działające na wahadło to naprężenie drążka T i siła grawitacji. Możemy więc zapisać siłę wypadkową jako:
F = T cos θ j − T sin θ i − m g j
Korzystając z prawa Newtona F = m a i przyspieszenia wahadła, które podaliśmy wcześniej, mamy
T cos θ j − T sin θ i − m g j = m R(θ'' cos θ i − θ' 2 sin θ i + θ'' sin θ j + θ' 2 cos θ j)
Rozpiszmy powyższe równanie na współrzędne. Daje nam to dwa równania: pierwsze dotyczące składowej i , a drugie składowej j .
−T sin θ = m R(θ'' cos θ − θ' 2 sin θ)
T cos θ − m g = m R(θ'' sin θ + θ' 2 cos θ)
Teraz kilka przekształceń algebraicznych, aby pozbyć się niewiadomej T . Mnożymy pierwsze równanie przez cos θ , a drugie przez sin θ .
−T sin θ cos θ = m R(θ'' cos2θ − θ' 2 sin θ cos θ)
T cos θ sin θ − m g sin θ = m R(θ'' sin2θ + θ' 2 sin θ cos θ)
Podstawiamy z pierwszego równania T cos θ sin θ do drugiego, aby po niewielkich przekształceniach otrzymać:
−θ'' cos2θ + θ' 2 sin θ cos θ = θ'' sin2θ + θ' 2 sin θ cos θ + g⁄R sin θ
Po skorzystaniu z tożsamości trygonometrycznej cos2θ + sin2θ = 1 upraszcza to równanie do postaci (1)
θ'' = − g⁄R sin θ
Zależności fizyczne - energia
Jest jeszcze trzeci sposób wyprowadzenia równań ruchu dla wahadła. Można zastosować "niebezpośrednią", opartą o analizę energii, metodę związaną z terminami takimi jak "lagranżjan", "Równania Eulera-Lagrange'a", "hamiltonian" i inne. Chociaż ta metoda nie jest tutaj pokazana, można zobaczyć przykład jej zastosowania w opisie symulacji Wózek + wahadło.
Rozwiązanie numeryczne
Aby rozwiązać równania ruchu numerycznie, żebyśmy mogli sterować symulacją, stosujemy metodę Rungego Kutty do rozwiązywania układów równań różniczkowych zwyczajnych. Najpierw definiujemy prędkość kątową ω = θ' . Następnie możemy zapisać równanie drugiego rzędu (1) jako dwa równania pierwszego rzędu.
θ' = ω
ω' = − g⁄R sin θ
Jest to forma, której potrzebujemy, aby użyć metody Rungego-Kutty.
Odpowiedzi
Pytanie: Jaki jest związek między przyspieszeniem kątowym a kątem?
θ'' = − g⁄R sin θ
Pytanie: Jak masa, długość oraz przyspieszenie grawitacyjne wpływa na zależność między przyspieszeniem kątowym a kątem?
- Masa w ogóle nie wpływa na ruch.
- Amplituda zależności sinusoidalnej jest proporcjonalna do przyspieszenia grawitacyjnego.
- Amplituda zależności sinusoidalnej jest odwrotnie proporcjonalna do długości wahadła.
Pytanie: Jak długość oraz przyspieszenie grawitacyjne, w przypadku małych oscylacji, wpływa na okres lub częstotliwość oscylacji?
θ'' = − g⁄R θ
Jest to zależność liniowa. Widać, że wykres przyspieszenia w funkcji kąta dla małych wychyleń jest linią prostą. Jest to analogiczna postać równania, co w przypadku symulacji pojedynczej sprężyny. Rozwiązaniem analitycznym jest
$$\theta(t) = \theta_0 \cos(\sqrt{g/R} \; t)$$
gdzie θ0 to kąt początkowy, a t to czas. Okres to czas po jakim faza zmienia się o 2π , więc
$$okres = \frac{2 \pi}{\sqrt{g/R}}$$
Częstotliwość drgań jest odwrotnością okresu:
$$częstotliwość = \frac{1}{2 \pi} \sqrt{g/R}$$
Możemy więc przewidywać, że
- czterokrotne zwiększenie długości podwaja okres i zmniejsza o połowę częstotliwość;
- czterokrotne zwiększenie przyspieszenia grawitacyjnego dwukrotnie zmniejsza okres i podwaja częstotliwość;
Jednostki miary
Symulacje myPhysicsLab nie mają określonych jednostek miary, takich jak metry, kilogramy, sekundy. Jednostki są bezwymiarowe, mogą być interpretowane, jak chcesz, ale muszą być spójne w symulacji.
Na przykład, jeśli traktujemy jednostkę odległości jako jeden metr i jednostkę czasu jako jedną sekundę, to jednostka prędkości musi wynosić jeden metr/sekundę.
Dostosuj i udostępnij
Istnieje kilka sposobów na odtworzenie określonej konfiguracji eksperymentalnej. Najłatwiej jest kliknąć przycisk „udostępnij”.
- Zmodyfikuj symulację, zmieniając parametry, takie jak grawitacja, tłumienie oraz przeciągając obiekty za pomocą myszy.
- Kliknij przycisk „udostępnij”. Skopiuj adres URL z okna dialogowego.
- Udostępnij adres URL lub zapisz go w pliku tekstowym do późniejszego wykorzystania.
Gdy odbiorca kliknie adres URL, EasyScript osadzony w tym adresie powieli warunki, które zostały ustawione.
Zobacz Dostosowywanie symulacji myPhysicsLab (en) jak dodatkowo programować symulacje z bezpośrednim wykorzystaniem JavaScript lub EasyScript.
Opublikowano po raz pierwszy w kwietniu 2001 roku.