Istnieją dwa sposoby znalezienia równań ruchu dla takiego układu: bezpośredni sposób newtonowski lub pośredni sposób Lagrange'a. Pokazujemy tutaj obie metody.
Kinematyka
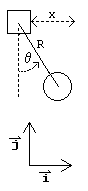
Zarówno w przypadku metody bezpośredniej, jak i pośredniej musimy najpierw uzyskać prawidłowy opis kinematyczny. Kinematyka oznacza tu relacje części urządzenia, bez względu na siły. W kinematyce staramy się tylko znaleźć wyrażenia określające położenia, prędkości i przyspieszenia w kategoriach dowolnych zmiennych, które wybraliśmy. Zmienne tutaj:
- x = położenie wózka (0 = sprężyna nierozciągnięta)
- θ = kąt wahadła (0 = wahadło zwisające w dół)
- R = długość pręta (stała)
Będziemy potrzebować wersorów osi, i, j, k . Do oznaczenia wektora używamy pogrubienia i kreski nad symbolem.
- i = (1,0,0) wektor jednostkowy w kierunku poziomym
- j = (0,1,0) wektor jednostkowy w kierunku pionowym
- k = (0,0,1) wektor jednostkowy w kierunku osi z (przed stronę w kierunku czytelnika)
Kinematyka wózka jest prosta
położenie = x i
prędkość = x' i
przyspieszenie = x'' i
Kinematyka wahadła jest bardziej złożona. Położenie uzyskuje się dzięki zastosowaniu dość prostej trygonometrii. Prędkość i przyspieszenie są pierwszą i drugą pochodną tego położenia.
położenie = x i + R sin θ i − R cos θ j
prędkość = x' i + R θ' cos θ i + R θ' sin θ j
przyspieszenie = x'' i + R θ'' cos θ i − R θ' 2 sin θ i + R θ'' sin θ j + R θ' 2 cos θ j
Siły
Traktujemy wózek i wahadło jako punkty materialne. Zaczniemy od narysowania diagramu sił działających na wózek i zapisania wyrażeń określających te siły. Wprowadzamy następujące oznaczenia:
- N = siła reakcji (podłoża, na którym znajduje się wózek)
- T = naprężenie pręta
- M = masa wózka
- m = masa wahadła
- g = przyspieszenie grawitacyjne
- d = stała tłumienia wózka
- b = stała tłumienia wahadła
- k = stała sprężystości sprężyny
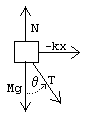siły działające na wózek
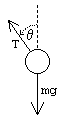
siły działające na wahadło
Wystarczy spojrzeć na diagram sił, aby w prosty sposób określić niektóre siły działające na wózek. (Siła tłumiąca wahadło jest trudniejsza, wyjaśniono to dalej).
- siła sprężyny = −k x i
- siła reakcji podłoża = N j
- siła grawitacyjna = −M g j
- naprężenie pręta = −T cos θ j + T sin θ i
- siła tłumiąca wózek = −d x' i
- siła tłumiąca wahadło (reakcja) = b⁄R θ' (cos θ i + sin θ j)
Siły działające na obciążnik wahadła to:
- naprężenie pręta = T cos θ j − T sin θ i
- siła grawitacyjna = −m g j
- siła tłumiąca wahadło = −b⁄R θ' (cos θ i + sin θ j)
Moment siły tłumiącej wahadło
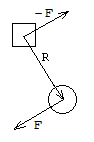
moment siły tłumiącej
Rozpatrujemy sytuację, w której moment siły tłumiącej wahadło jest wektorem prostopadłym do płaszczyzny, w której porusza się wahadło i wózek. Oznacza to, że moment obrotowy ma kierunek wektora jednostkowego k, skierowanego przed płaszczyznę. Wartość momentu obrotowego jest dana przez wartość bezwzględną −b θ', gdzie θ' jest prędkością kątową. Możemy uznać siłę z momentu obrotowego za odpowiadającą sile przyłożonej na końcu pręta wahadła (patrz ilustracja). Z trzeciej zasady dynamiki Newtona (każdej sile akcji odpowiada równa co do wartości i o przeciwnym zwrocie siła reakcji) wiemy, że taka sama siła jest przyłożona w drugim końcu pręta (działa na wózek), ale w przeciwnym kierunku.
Moment siły F przyłożonej do końca pręta R jest iloczynem wektorowym
R × F = (Rx, Ry, 0) × (Fx, Fy, 0) = (Rx Fy − Ry Fx) k
Tutaj zapisujemy trójwymiarowy wektor w postaci (x, y, z) co jest równoważne zapisowi x i + y j + z k . Traktujemy siłę F jako prostopadłą do pręta, więc
F = f (−Ry, Rx, 0) ⁄ R
gdzie f jest nieznaną wartością F , a R jest wartością R tak że R = √(Rx2 + Ry2) . Zwrot wektora F jest tak dobrany, że moment obrotowy o zwrocie zgodnym ze zwrotem osi z prowadzi do zwiększenia θ . Zatem iloczyn wektorowy przyjmuje postać
R × F = (Rx Fy − Ry Fx) k = f (Rx2 + Ry2) ⁄ R k = f R k
Teraz możemy wyznaczyć f :
−b θ' k = R × F = f R k
f = −b⁄R θ'
Wynik ten ma sens: zauważ, że aby uzyskać określoną wartość momentu obrotowego, potrzebna byłaby większa siła przyłożona na końcu krótkiego pręta lub mniejsza siła przy dłuższym pręcie. Siła jest zatem dana przez
F = f (−Ry, Rx, 0) ⁄ R = −b⁄R θ' (cos θ i + sin θ j)
Zauważ, że R = R(sin θ, −cos θ, 0) co uzasadnia część powyższego równania. Ta siła F jest przyłożona do obciążnika wahadła, a a siła reakcji do niej przeciwna jest przyłożona do wózka.
Bezpośrednia metoda znajdowania równań ruchu
Sumujemy siły opisane powyżej, aby znaleźć siłę wypadkową działającą na wózek
F = N j − M g j − T cos θ j + T sin θ i − k x i − d x' i + b⁄R θ' (cos θ i + sin θ j)
Teraz korzystając z II zasady dynamiki Newtona F = M a i przyspieszenia wózka, które znaleźliśmy wcześniej, mamy
| N j − M g j − T cos θ j + T sin θ i − k x i + b⁄R θ' (cos θ i + sin θ j) = M x'' i | (1) |
Zsumowanie sił działających na wahadło daje
F = T cos θ j − T sin θ i − m g j − b⁄R θ' (cos θ i + sin θ j)
Korzystając z II zasady dynamiki Newtona F = m a i przyspieszenia wahadła, które znaleźliśmy wcześniej, mamy
| T cos θ j − T sin θ i − m g j − b⁄R θ' (cos θ i + sin θ j) = m(x'' i + R θ'' cos θ i − R θ' 2 sin θ i + R θ'' sin θ j + R θ' 2 cos θ j) | (2) |
Teraz możemy zapisać powyższe równania (1) i (2) jako oddzielne równania dla poszczególnych składowych. Daje nam to układ 4 równań.
| T sin θ − k x − d x' + b⁄R θ' cos θ = M x'' | (3) |
N − M g − T cos θ + b⁄R θ' sin θ = 0
| − T sin θ − b⁄R θ' cos θ = m(x'' + R θ'' cos θ − R θ' 2 sin θ) | (4) |
| T cos θ − m g − b⁄R θ' sin θ = m(R θ'' sin θ + R θ' 2 cos θ) | (5) |
(Zignorujemy drugie z czterech równań, ale możemy użyć go do znalezienia nieznanej siły reakcji podłoża N działającej na wózek). Następnie wykonujemy kilka przekształceń algebraicznych, aby wyeliminować nieznane naprężenie T . Sumując równania (3) i (4), po przekształceniach otrzymujemy:
| (M + m)x'' = m R θ' 2 sin θ − m R θ'' cos θ − k x − d x' | (6) |
Mnożymy równanie (5) przez sin θ
T sin θ cos θ − m g sin θ − b⁄R θ' sin2 θ = m R θ'' sin2 θ + m R θ' 2sin θ cos θ
Z równania (4) podstawiamy T sin θ .
−b⁄R θ' cos2 θ − m x'' cos θ − m R θ'' cos2θ + m R θ' 2sin θ cos θ − m g sin θ − b⁄R θ' sin2 θ = m R θ'' sin2θ + m R θ' 2sin θ cos θ
Wykorzystanie tożsamości trygonometrycznej cos2θ + sin2θ = 1 upraszcza to do
| b⁄R θ' + m x'' cos θ + m R θ'' + m g sin θ = 0 | (7) |
Równania (6) i (7) są równaniami ruchu. Mamy dwa równania dwóch zmiennych x, θ i ich pochodnych. Będziemy musieli wykonać kilka dalszych przekształceń tych dwóch równań, aby uzyskać formę odpowiednią dla metody analizy numerycznej Rungego-Kutty (patrz poniżej).
Metoda pośrednia (energetyczna) znajdowania równań ruchu
Metoda pośrednia opiera się na energii układu. Naszym pierwszym krokiem będzie znalezienie Lagranżjanu układu, który jest różnicą energii kinetycznej i energii potencjalnej.
L = T − V
- L = Lagranżjan
- T = energia kinetyczna
- V = energia potencjalna
Do energii kinetycznej potrzebujemy prędkości wózka i wahadła, które obliczyliśmy wcześniej (zobacz kinematyka powyżej). Energia kinetyczna jest dana przez 1⁄2m v2 . Zauważ, że używamy iloczynu skalarnego do obliczenia kwadratu wektora, v2 = v · v . Tak więc mamy
T = 1⁄2 M (x' i)2 + 1⁄2 m (x' i + R θ' cos θ i + R θ' sin θ j)2
Stosując definicję iloczynu skalarnego do obliczenia kwadratu wektora otrzymujemy
T = 1⁄2 M x' 2 + 1⁄2 m ((x' + R θ' cos θ)2 + (R θ' sin θ)2)
Mamy dwa elementy magazynujące energię potencjalną w tym układzie: sprężyna (energia sprężystości) i obciążnik wahadła (energia grawitacyjna).
Vsprężystości = 1⁄2 k x2
Vgrawitacji = m g wysokość = m g(R − R cos θ)
Zatem Lagranżjanem dla układu jest
L = M⁄2 x' 2 + m⁄2 (x' + R θ' cos θ)2 + m⁄2 (R θ' sin θ)2 − k⁄2 x2 − m g R(1 − cos θ)
Siły uogólnione: opór
Aby poradzić sobie z siłami oporu, obliczamy wielkość niezachowawczej pracy wykonanej przy małych ruchach zmiennych. Zauważ, że rozważamy tu tylko siły niezachowawcze, takie jak opór -- siły zachowawcze, takie jak siła grawitacji lub sprężystości, są uwzględnione przez obliczenia energii potencjalnej w Lagranżjanie.
Mała zmiana Δx dotycząca x prowadzi do wykonania przez siłę oporu pewnej niezachowawczej pracy danej przez ΔW = −d x' Δx więc definiujemy „siłę uogólnioną ”
Wx = −d x'
Podobnie mała zmiana Δθ dotycząca θ prowadzi do wykonania przez siłę oporu pewnej niezachowawczej pracy ΔW = −b θ' Δθ , więc definiujemy następną siłę uogólnioną:
Wθ = −b θ'
Równania ruchu z Lagranżjanu
Następnie z równania Lagrange'a wyprowadzimy równania ruchu. Dla zmiennej x równanie Lagrange'a to
$$W_x = \frac{d}{dt} \left( \frac{\partial L}{\partial x'} \right) - \frac{\partial L}{\partial x} \tag{8}$$
Zauważ, że x' i x są traktowane jako oddzielne zmienne przy liczeniu pochodnych cząstkowych. Oto te pochodne:
| ∂ L | = M x' + m(x' + R θ' cos θ) |
| ∂ x' |
| ∂ L | = − k x |
| ∂ x |
Biorąc pochodną \( \frac{\partial L}{\partial x'} \) po czasie i odejmując \( \frac{\partial L}{\partial x} \) przekształcamy równanie (8) do postaci
− d x' = M x'' + m x'' + m R θ'' cos θ − m R θ' 2 sin θ + k x
co można zapisać tak, aby było identyczne z równaniem (6) znalezionym wyżej, w metodzie bezpośredniej:
(M + m)x'' = m R θ' 2 sin θ − m R θ'' cos θ − k x − d x'
Dla zmiennej θ równanie Lagrange'a to
$$W_{\theta} = \frac{d}{dt} \left( \frac{\partial L}{\partial \theta'} \right) - \frac{\partial L}{\partial \theta} \tag{9}$$
Oto pochodne cząstkowe:
| ∂ L | = m(x' + R θ' cos θ)R cos θ + m θ' R2 sin2θ |
| ∂ θ' |
| ∂ L | = −m(x' + R θ' cos θ)R θ' sin θ + m R2 θ' 2sin θ cos θ − m g R sin θ |
| ∂ θ |
(Zauważ, że z każdego z tych wyrażeń możemy wyłączyć przed nawias wspólny czynnik m R.) Biorąc pochodną \( \frac{\partial L}{\partial \theta'} \) po czasie i odejmując \( \frac{\partial L}{\partial \theta} \) przekształcamy równanie (9) do postaci
− b θ' = m R [(x'' + R θ'' cos θ − R θ' 2 sin θ)cos θ − θ' sin θ(x' + R θ' cos θ) + θ'' R sin2θ + 2 θ' 2R sin θ cos θ + (x' + R θ' cos θ)θ' sin θ − R θ' 2sin θ cos θ + g sin θ]
Po redukcji i skorzystaniu z tożsamości sin2θ + cos2θ = 1 upraszcza się to do równania (7) z metody bezpośredniej:
b⁄R θ' + m x'' cos θ + m R θ'' + m g sin θ = 0
Którą technikę wolisz, bezpośrednią czy pośrednią? Wydaje się, że metoda pośrednia jest wyborem inżynierów mechaników. Wymaga więcej rachunku różniczkowego, ale obliczenia są dużo łatwiejsze. Porównaj to, co zostało zrobione tutaj, z wcześniejszymi obliczeniami dotyczącymi momentu oporu w metodzie bezpośredniej. Z drugiej strony, metoda bezpośrednia jest niezbędna do określenia sił w układzie, takich jak naprężenie pręta lub siła reakcji toru na wózek.
Rozwiązanie numeryczne
Aby rozwiązać równania ruchu numerycznie, żebyśmy mogli sterować symulacją, stosujemy metodę Rungego Kutty do rozwiązywania układów równań różniczkowych zwyczajnych.
Aby użyć metody Runge-Kutta, musimy przekształcić równania (6) i (7) do następującej formy:
x'' = f(x, x', θ, θ')
θ'' = g(x, x', θ, θ')
gdzie f, g są funkcjami, które należy określić. Chcemy też wyrazić każdą drugą pochodną za pomocą niższych pochodnych. Jeśli spojrzymy wstecz na równania (6) i (7), zobaczymy, że wymagają pewnych przekształceń, aby wyizolować drugie pochodne po lewej stronie. Po wyznaczeniu θ'' i x'' (albo samodzielnie, albo za pomocą programu algebry, takiego jak Mathematica) otrzymujemy:
| x'' = | m R θ' 2 sin θ + m g sin θ cos θ − k x − d x' + b⁄R θ' cos θ |
| M + m sin2θ |
| θ'' = | −m R θ' 2 sin θ cos θ − (m+M)g sin θ + k x cos θ + d x' cos θ − (1 + M⁄m)b⁄R θ' |
| R (M + m sin2θ) |
Jeśli zdefiniujemy kilka nowych zmiennych, możemy to zmienić na cztery równania pierwszego rzędu (to znaczy cztery równania tylko z pierwszymi pochodnymi).
- v = prędkość wózka
- ω = prędkość kątowa wahadła
x' = v
θ' = ω
| v' = | m R ω2 sin θ + m g sin θ cos θ − k x − d v + b⁄R ω cos θ |
| M + m sin2θ |
| ω' = | −m R ω2 sin θ cos θ − (m+M)g sin θ + k x cos θ + d v cos θ − (1 + M⁄m)b⁄R ω |
| R (M + m sin2θ) |
Jest to dokładnie ta forma, której potrzebujemy, aby użyć metody Rungego-Kutty do numerycznego rozwiązania układu.
Jednostki miary
Symulacje myPhysicsLab nie mają określonych jednostek miary, takich jak metry, kilogramy, sekundy. Jednostki są bezwymiarowe, mogą być interpretowane, jak chcesz, ale muszą być spójne w symulacji.
Na przykład, jeśli traktujemy jednostkę odległości jako jeden metr i jednostkę czasu jako jedną sekundę, to jednostka prędkości musi wynosić jeden metr/sekundę.
Dostosuj i udostępnij
Istnieje kilka sposobów na odtworzenie określonej konfiguracji eksperymentalnej. Najłatwiej jest kliknąć przycisk „udostępnij”.
- Zmodyfikuj symulację, zmieniając parametry, takie jak grawitacja, tłumienie oraz przeciągając obiekty za pomocą myszy.
- Kliknij przycisk „udostępnij”. Skopiuj adres URL z okna dialogowego.
- Udostępnij adres URL lub zapisz go w pliku tekstowym do późniejszego wykorzystania.
Gdy odbiorca kliknie adres URL, EasyScript osadzony w tym adresie powieli warunki, które zostały ustawione.
Zobacz Dostosowywanie symulacji myPhysicsLab (en) jak dodatkowo programować symulacje z bezpośrednim wykorzystaniem JavaScript lub EasyScript.
Opublikowano po raz pierwszy we wrześniu 2001 roku.
