W przypadku małych kątów wahadło zachowuje się jak układ liniowy (zobacz wahadło proste). Gdy kąty są małe w podwójnym wahadle, układ zachowuje się analogicznie do zachowania liniowego podwójnej sprężyny. Na wykresie możemy obserwować powstawanie podobnych krzywych Lissajous. Dzieje się tak, ponieważ ruch jest określony przez proste funkcje sinus i cosinus.
W przypadku dużych kątów wahadło jest nieliniowe, a wykres fazowy staje się znacznie bardziej złożony. Widać to, gdy przeciągniemy jedną masę, odchylając o większy kąt i puścimy.
Przyjmujemy, że pręty wahadła są pozbawione masy i sztywne. Obciążniki traktujemy jako punkty materialne. Wyprowadzenie równań ruchu, przy użyciu bezpośredniej metody newtonowskiej, pokazano poniżej.
Kinematyka podwójnego wahadła
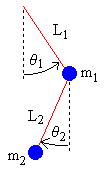
Kinematyka oznacza tu relacje części urządzenia, bez względu na siły. W kinematyce staramy się tylko znaleźć wyrażenia określające położenia, prędkości i przyspieszenia w kategoriach zmiennych, które określają stan urządzenia.
- x = położenie masy wahadła w poziomie
- y = położenie masy wahadła w pionie
- θ = kąt wahadła (0 = odpowiada położeniu pionowemu w dół, przy wychyleniu przeciwnym do ruchu wskazówek zegara jest dodatni)
- L = długość pręta (stała)
Początek układu współrzędnych umieszczamy w punkcie zaczepienia górnego wahadła. Przyjmujemy, że oś y jest skierowana do góry, a x w prawo. Oznaczamy wielkości dotyczące górnego wahadła indeksem 1, a dolnego indeksem 2. Zacznijmy od prostych związków trygonometrycznych, aby zapisać wyrażenia określające położenia x1, y1, x2, y2 w zależności od kątów θ1, θ2 .
x1 = L1 sin θ1
y1 = −L1 cos θ1
x2 = x1 + L2 sin θ2
y2 = y1 − L2 cos θ2
Prędkość jest pochodną położenia po czasie.
x1' = θ1' L1 cos θ1
y1' = θ1' L1 sin θ1
x2' = x1' + θ2' L2 cos θ2
y2' = y1' + θ2' L2 sin θ2
Przyspieszenie jest drugą pochodną.
| x1'' = −θ1'2 L1 sin θ1 + θ1'' L1 cos θ1 | (1) |
| y1'' = θ1'2 L1 cos θ1 + θ1'' L1 sin θ1 | (2) |
| x2'' = x1'' − θ2'2 L2 sin θ2 + θ2'' L2 cos θ2 | (3) |
| y2'' = y1'' + θ2'2 L2 cos θ2 + θ2'' L2 sin θ2 | (4) |
Siły działające na podwójne wahadło
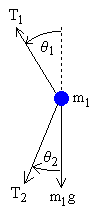
górna masa
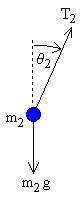
dolna masa
Traktujemy oba obciążniki wahadła jako punkty materialne. Zaczniemy od narysowania schematu sił dla górnej masy i zapisania wyrażenia na działającą na nią siłę wypadkową. Wprowadzamy następujące zmienne:
- T = naprężenie pręta
- m = masa wahadła
- g = przyspieszenie grawitacyjne
Siły działające na górną masę wahadła to naprężenie górnego pręta T1 , naprężenie dolnego pręta T2 i siła grawitacji −m1 g . Zapiszemy osobne równania dla składowych poziomych i pionowych, ponieważ można je traktować niezależnie. Siła wypadkowa działająca na masę jest ich sumą. Stosujemy drugą zasadę dynamiki Newtona F = m a .
| m1 x1'' = −T1 sin θ1 + T2 sin θ2 | (5) |
| m1 y1'' = T1 cos θ1 − T2 cos θ2 − m1 g | (6) |
W przypadku dolnej masy, działające siły to naprężenie dolnego pręta T2 i siła grawitacji −m2 g .
| m2 x2'' = −T2 sin θ2 | (7) |
| m2 y2'' = T2 cos θ2 − m2 g | (8) |
Odnosząc te równania do schematów sił, należy pamiętać, że na przykład na górnym schemacie sił θ1 jest dodatni, a θ2 jest ujemny, zgodnie z konwencją, że kąt skierowany przeciwnie do ruchu wskazówek zegara jest dodatni, a zgodnie ujemny (tu od osi OY).
Bezpośrednia metoda znajdowania równań ruchu
Teraz wykonamy pewne przekształcenia algebraiczne w celu znalezienia równań wyrażających θ1'', θ2'' w zależności od θ1, θ1', θ2, θ2' . Zacznijmy od wyznaczenia z równań (7), (8) T2 sin θ2 i T2 cos θ2 , a następnie podstawienia do równań (5) i (6).
| m1 x1'' = −T1 sin θ1 − m2 x2'' | (9) |
| m1 y1'' = T1 cos θ1 − m2 y2'' − m2 g − m1 g | (10) |
Mnożymy teraz równanie (9) prez cos θ1 , a równanie (10) przez sin θ1 i po przekształceniach otrzymujemy
| T1 sin θ1 cos θ1 = −cos θ1 (m1 x1'' + m2 x2'') | (11) |
| T1 sin θ1 cos θ1 = sin θ1 (m1 y1'' + m2 y2'' + m2 g + m1 g) | (12) |
To prowadzi do równania
| sin θ1 (m1 y1'' + m2 y2'' + m2 g + m1 g) = −cos θ1 (m1 x1'' + m2 x2'') | (13) |
Następnie mnożymy równanie (7) przez cos θ2 , a równanie (8) przez sin θ2 i przekształcamy, aby uzyskać
| T2 sin θ2 cos θ2 = −cos θ2 (m2 x2'') | (14) |
| T2 sin θ2 cos θ2 = sin θ2 (m2 y2'' + m2 g) | (15) |
co prowadzi do
| sin θ2 (m2 y2'' + m2 g) = −cos θ2 (m2 x2'') | (16) |
Następnie musimy użyć systemu algebry komputerowej do wyznaczenia z równań (13) i (16) θ1'', θ2'' w zależności od θ1, θ1', θ2, θ2' . Zauważ, że dołączamy również definicje dane równaniami (1-4), tak że mamy 2 równania (13, 16) i 2 niewiadome ( θ1'', θ2'' ). Wynik jest nieco skomplikowany, ale jest łatwy do zaprogramowania w komputerze.
| θ1'' = | −g (2 m1 + m2) sin θ1 − m2 g sin(θ1 − 2 θ2) − 2 sin(θ1 − θ2) m2 (θ2'2 L2 + θ1'2 L1 cos(θ1 − θ2)) |
| L1 (2 m1 + m2 − m2 cos(2 θ1 − 2 θ2)) |
| θ2'' = | 2 sin(θ1 − θ2) (θ1'2 L1 (m1 + m2) + g(m1 + m2) cos θ1 + θ2'2 L2 m2 cos(θ1 − θ2)) |
| L2 (2 m1 + m2 − m2 cos(2 θ1 − 2 θ2)) |
Są to równania ruchu podwójnego wahadła.
Rozwiązanie numeryczne
Powyższe równania mają już formę bliską tej, której potrzebujemy, żeby zastosować meodę Rungego Kutty. Ostatnim krokiem jest przekształcenie tych dwóch równań drugiego rzędu na cztery równania pierwszego rzędu. Określimy następujące pierwsze pochodne jako odrębne zmienne:
- ω1 = prędkość kątowa górnego pręta
- ω2 = prędkość kątowa dolnego pręta
Teraz możemy zapisać cztery równania pierwszego rzędu:
θ1' = ω1
θ2' = ω2
| ω1' = | −g (2 m1 + m2) sin θ1 − m2 g sin(θ1 − 2 θ2) − 2 sin(θ1 − θ2) m2 (ω22 L2 + ω12 L1 cos(θ1 − θ2)) |
| L1 (2 m1 + m2 − m2 cos(2 θ1 − 2 θ2)) |
| ω2' = | 2 sin(θ1−θ2) (ω12 L1 (m1 + m2) + g(m1 + m2) cos θ1 + ω22 L2 m2 cos(θ1 − θ2)) |
| L2 (2 m1 + m2 − m2 cos(2 θ1 − 2 θ2)) |
Jest to dokładnie ta forma, której potrzebujemy, aby użyć metody Rungego-Kutty do numerycznego rozwiązania układu.
Jednostki miary
Symulacje myPhysicsLab nie mają określonych jednostek miary, takich jak metry, kilogramy, sekundy. Jednostki są bezwymiarowe, mogą być interpretowane, jak chcesz, ale muszą być spójne w symulacji.
Na przykład, jeśli traktujemy jednostkę odległości jako jeden metr i jednostkę czasu jako jedną sekundę, to jednostka prędkości musi wynosić jeden metr/sekundę.
Dostosuj i udostępnij
Istnieje kilka sposobów na odtworzenie określonej konfiguracji eksperymentalnej. Najłatwiej jest kliknąć przycisk „udostępnij”.
- Zmodyfikuj symulację, zmieniając parametry, takie jak grawitacja, tłumienie oraz przeciągając obiekty za pomocą myszy.
- Kliknij przycisk „udostępnij”. Skopiuj adres URL z okna dialogowego.
- Udostępnij adres URL lub zapisz go w pliku tekstowym do późniejszego wykorzystania.
Gdy odbiorca kliknie adres URL, EasyScript osadzony w tym adresie powieli warunki, które zostały ustawione.
Zobacz Dostosowywanie symulacji myPhysicsLab (en) jak dodatkowo programować symulacje z bezpośrednim wykorzystaniem JavaScript lub EasyScript.
Opublikowano po raz pierwszy w lutym 2002 roku.