Dwie symulacje w jednym
Mamy tutaj dwie oddzielne, ale powiązane symulacje:
- Blok kotwiczący jest modelowany jako punkt materialny, który może swobodnie poruszać się w kierunkach x i y, z dużym tłumieniem (oporem) i bez grawitacji. W ten sposób użytkownik może przeciągnąć blok kotwiczący zgodnie z potrzebami, używając prostej siły typu „gumka” między położeniem kursora a blokiem. W pionie na blok może także działać zewnętrzna siła okresowa. Zakładamy, że masa bloku kotwiczącego jest znacznie większa niż masa wahadła, tak że do obliczenia jego dynamiki możemy zignorować ruch wahadła.
- Wahadło przejmuje ruch punktu kotwiczenia jako dane. Na wahadło działa siła grawitacji i oporu, o wartościach, które są niezależne od wartości używanych do symulacji bloku kotwiczącego.
Kinematyka wahadła z ruchomym punktem zaczepienia
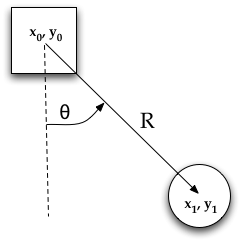
zmienne wahadła
Kinematyka oznacza tu relacje części urządzenia, bez względu na siły. W kinematyce staramy się tylko znaleźć wyrażenia określające położenia, prędkości i przyspieszenia w kategoriach zmiennych, które określają stan urządzenia.
- \( (x_0, y_0) = \) położenie punktu zaczepienia
- \( (x_1, y_1) = \) położenie środka masy wahadła
- \( R = \) długość pręta (stała)
- \( \theta = \) kąt wahadła (\( \theta = 0 \) odpowiada położeniu pionowemu w dół, przy wychyleniu przeciwnym do ruchu wskazówek zegara jest dodatni)
- \( \theta' = \) prędkość kątowa
- \( \theta'' = \) przyspieszenie kątowe
Przyjmujemy, że oś \( y \) jest skierowana do góry, a \( x \) w prawo. Zacznijmy od prostych związków trygonometrycznych, aby zapisać wyrażenia na położenie wahadła \( x_1, y_1 \) w zależności od kąta \( \theta \) i położenia punktu zaczepienia \( x_0, y_0 \).
$$x_1 = x_0 + R \sin (\theta) \tag{1}$$
$$y_1 = y_0 - R \cos(\theta) \tag{2}$$
Prędkość jest pochodną położenia po czasie.
$$x_1' = x_0' + \theta' R \cos(\theta) \tag{3}$$
$$y_1' = y_0' + \theta' R \sin(\theta) \tag{4}$$
Przyspieszenie jest drugą pochodną położenia po czasie.
$$x_1'' = x_0'' - \theta'^2 R \sin(\theta) + \theta'' R \cos(\theta) \tag{5}$$
$$y_1'' = y_0'' + \theta'^2 R \cos(\theta) + \theta'' R \sin(\theta) \tag{6}$$
Siły działające na wahadło z ruchomym punktem zaczepienia
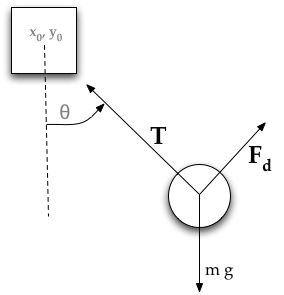
diagram sił
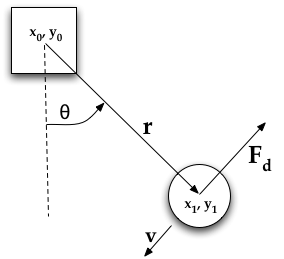
siła tłumienia Fd
Traktujemy obciążnik wahadła jako punkt materialny. Narysowanie sił działających na obciążnik pomoże nam zapisać wyrażenie na siłę wypadkową. Wprowadzamy następujące zmienne:
- \( T = \) naprężenie pręta
- \( m = \) masa wahadła
- \( g = \) przyspieszenie grawitacyjne
- \( b = \) stała tłumienia (oporu)
- \( F_d = \) siła tłumienia
Siły działające na obciążnik to naprężenie pręta \( T \), siła tłumiąca \( F_d \) i siła grawitacyjna \( -m\;g \). Zapiszemy osobne równania dla składowych poziomych i pionowych, ponieważ można je traktować niezależnie. Siła wypadkowa jest ich sumą.
Z diagramu sił (po lewej), po dokonaniu rozkładu, możemy odczytać, że równania zależności siła - przyspieszenie (z II zasady dynamiki Newtona \( \mathbf{F} = m \mathbf{a} \)) będą następujące:
$$ m \; x_1''= - T \sin(\theta) + F_d \cos(\theta)$$
$$ m \; y_1''= T \cos(\theta) + F_d \sin(\theta) - m \; g$$
Musimy tylko znaleźć siłę tłumiącą. Zakładamy, że siła tłumienia jest dana prostą zależnością - jej moment obrotowy jest proporcjonalny do prędkości kątowej i przeciwnie skierowany:
$$\tau = - b \; \theta'$$
Tu długość wahadła nie ma znaczenia, dla wartości momentu obrotowego. (Różni się to od działania systemu engine2D, gdzie tłumienie jest związane z ruchem postępowym w przestrzeni, jak również z ruchem obrotowym.)
Z podręcznika fizyki wiemy, że moment obrotowy działający na cząstkę jest zdefiniowany jako iloczyn wektorowy ramienia siły i siły
$$\tau = \mathbf{r} \times \mathbf{F}$$
Jeden ze sposobów spojrzenia na powyższe równanie: dany moment obrotowy można uzyskać przykładając mniejszą siłę o większej wartości ramienia lub większą siłę o mniejszym ramieniu. Moment obrotowy jest wielkością wektorową. Jego wartość jest określona przez
$$|\tau| = r F \sin(\gamma)$$
gdzie \( \gamma \) jest kątem pomiędzy \( \mathbf{r} \) i \( \mathbf{F} \). W naszym przypadku zawsze \( \gamma = \pm \pi/2 \) rad = \( \pm 90 \) stopni. Możemy teraz zapisać wartość momentu obrotowego następującym wzorem:
$$|\tau| = R F_d = -b \theta' $$
Następnie wyznaczamy z tego wzoru siłę tłumienia
$$F_d = -\frac{b}{R} \theta'$$
Powyższe jest tylko wartością siły tłumienia. Zapis wektorowy wygląda następująco:
$$\mathbf{F}_d = -\frac{b}{R} \theta' (\cos(\theta) \mathbf{i} + \sin(\theta) \mathbf{j})$$
Teraz możemy dodać wszystkie siły: naprężenie T pręta, siłę tłumiącą i grawitacyjną, i wyrazić je w dwuwymiarowych współrzędnych kartezjańskich, x i y. Tutaj pokazujemy siłę wypadkową i stosujemy drugą zasadę dynamiki Newtona \( \mathbf{F} = m \; \mathbf{a} \).
$$ m \; x_1''= - T \sin(\theta) - \frac{b}{R} \theta' \cos(\theta) \tag{7}$$
$$ m \; y_1''= T \cos(\theta) - \frac{b}{R} \theta' \sin(\theta) - m \; g \tag{8}$$
Bezpośrednia metoda znajdowania równań ruchu
Teraz wykonamy pewne przekształcenia algebraiczne w celu znalezienia równania ruchu wahadła, które będzie wyrażało \( \theta'' \) w zależności od \( \theta, \theta' \). Mnożymy równanie (7) przez \( \cos(\theta) \), a równanie (8) przez \(\sin(\theta)\).
$$ \cos(\theta) m \; x_1''= - T \sin(\theta) \cos(\theta) - \frac{b}{R} \theta' \cos^2(\theta) \tag{9}$$
$$ \sin(\theta) m \; y_1''= T \sin(\theta) \cos(\theta) - \frac{b}{R} \theta' \sin^2(\theta) - m \; g \; \sin(\theta) \tag{10}$$
Dodając te dwa równania otrzymamy
$$ \cos(\theta) \;m\; x_1'' + \sin(\theta) m \; y_1''= - \frac{b}{R} \theta' - m \; g \; \sin(\theta) \tag{11}$$
Następnie podstawiamy \( x_1'' \) i \( y_1'' \) z równań (5) i (6)
$$\begin{multline} \cos(\theta) \;m \Bigl(x_0'' - \theta'^2 R \sin(\theta) + \theta'' R \cos(\theta) \Bigr)\\ + \sin(\theta) m \Bigl(y_0'' + \theta'^2 R \cos(\theta) + \theta'' R \sin(\theta) \Bigr)\\ = - \frac{b}{R} \theta' - m \; g \; \sin(\theta) \end{multline} \tag{12}$$
co upraszcza się do
$$\cos(\theta) \;m\; x_0'' + \sin(\theta) m \;y_0'' + m\; R\; \theta'' = - \frac{b}{R} \theta' - m\; g\; \sin(\theta) \tag{13}$$
Przekształcenie tego daje równanie ruchu dla wahadła z ruchomym punktem zaczepienia
$$\theta'' = -\frac{\cos(\theta)}{R} x_0'' - \frac{\sin(\theta)}{R} y_0'' - \frac{b}{m R^2} \theta' - \frac{g}{R} \sin(\theta) \tag{14}$$
Pierwsze dwa wyrażenia związane są z ruchem punktu zaczepienia, \( (x_0, y_0) \). Zauważmy, że ruch punktu zaczepienia traktujemy jako „dany”, zgodnie z naszym założeniem, że blok kotwiczący jest znacznie masywniejszy od wahadła. Następna sekcja rozważa oddzielną symulację ruchu bloku kotwiczącego.
Następne wyrażenie, \( -\frac{b}{m R^2} \theta' \), pochodzi z siły tłumiącej.
Ostatnie wyrażenie, \( -(g/R) \sin(\theta) \), związane jest z siłą grawitacji.
Dynamika bloku kotwiczącego
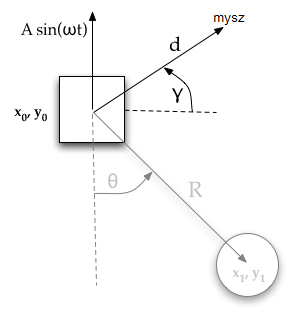
siły działające na blok
Blok kotwiczący ma własną oddzielną dynamikę, niezależną od wahadła. Ponieważ zakładamy, że jego masa jest znacznie większa od masy wahadła, ignorujemy wpływ ruchu wahadła na blok. Modelujemy kotwicę jako punkt materialny, podlegający działaniu: dużej siły tłumiącej, siły typu „gumka” sterowanej myszą i opcjonalnej pionowej siły oscylacyjnej.
- \( b_0 = \) stała tłumienia ruchu punktu kotwiczącego
- \( k = \) współczynnik sprężystości „gumki” myszy (\( k=0 \) gdy przycisk myszy nie jest wciśnięty)
- \( d = \) odległość od punktu zaczepienia wahadła do kursora
- \( \gamma = \) kąt między kierunkiem punkt zaczepienia - kursor, a poziomem (\( \gamma = 0 \) oznacza, że kursor myszy jest dokładnie na prawo od punktu zaczepienia)
- \( A = \) amplituda pionowej siły wymuszającej
- \( \omega = \) częstość kołowa pionowej siły wymuszającej
Siła tłumienia jest równa \( -b_0 \mathbf{v_0} \) gdzie \( \mathbf{v_0} = (x_0', y_0') \) jest prędkością bloku kotwiczącego.
Okresowo zmienna, pionowa siła wymuszająca ma postać \( A \sin(\omega t) \) gdzie \( t = \) to czas. Parametry \( A \) i \( \omega \) można ustawić za pomocą suwaków w panelu sterującym symulacji powyżej (występują pod nazwą amplituda napędu i częstość kołowa napędu).
Siła gumki myszy jest modelowana jako siła sprężyny o zerowej długości spoczynkowej; ma wartość \( k \; d \) i kierunek wzdłuż linii od bloku kotwiczącego do kursora, tworzący kąt \( \gamma \) z poziomem.
Uwzględniając te siły w II zasadzie dynamiki Newtona \( \mathbf{F} = m \; \mathbf{a} \), możemy zapisać równania ruchu dla punktu zakotwiczenia:
$$x_0'' = -b_0 x_0' + k d \cos(\gamma) \tag{15}$$
$$y_0'' = -b_0 y_0' + k d \sin(\gamma) + A \sin(\omega t) \tag{16}$$
(Pominęliśmy wszelkie wzmianki o masie bloku kotwiczącego; możemy założyć, jego że masa wynosi 1).
Siłę ze strony myszy rozłożyliśmy na składowe:
$$k d \cos(\gamma) = k (x_\text{kursor} - x_0)$$
$$k d \sin(\gamma) = k (y_\text{kursor} - y_0)$$
Zauważ, że kąt ustawienia wahadła \( \theta \) nie ma wpływu na równania (15) i (16). Oznacza to, że ruch wahadła nie wpływa na punkt kotwiczenia. Jest to uzasadnione, ponieważ przyjęliśmy, że blok kotwiczący jest znacznie bardziej masywny od wahadła.
Równania (14), (15) i (16) określają nasz model matematyczny ruchomego wahadła.
W zasadzie dokonaliśmy tylko jednej małej prostej zmiany w opisie kinematycznym w równaniach (1) i (2), którą było dodanie \( x_0 \) i \( y_0 \). To jest istotna różnica matematyczna w stosunku do wyprowadzenia dotyczącego standardowego wahadła. W tym drugim założyliśmy, że punkt zaczepienia wahadła jest ustalony (i stąd mogliśmy rozważać obrót wokół ustalonej osi).
Rozwiązanie numeryczne
Równania (14), (15), i (16) mają już formę bliską tej, której potrzebujemy, żeby zastosować meodę Rungego Kutty. Ostatnim krokiem jest przekształcenie tych trzech równań drugiego rzędu na sześć równań pierwszego rzędu. Określimy następujące pierwsze pochodne jako odrębne zmienne:
- \( \Omega = \theta' \) prędkość kątowa
- \( v_{x_0} = x_0' \) składowa x prędkości punktu kotwiczenia
- \( v_{y_0} = y_0' \) składowa y prędkości punktu kotwiczenia
Następnie możemy zapisać sześć równań pierwszego rzędu:
$$\begin{multline} \theta' = \Omega \end{multline}$$ $$\begin{multline} \Omega' = -\frac{\cos(\theta)}{R} v_{x_0}' - \frac{\sin(\theta)}{R} v_{y_0}' - \frac{b}{m R^2} \Omega - \frac{g}{R} \sin(\theta) \end{multline}$$ $$\begin{multline} x_0' = v_{x_0} \end{multline}$$ $$\begin{multline} v_{x_0}' = -b_0 v_{x_0} + k (x_\text{kursor} - x_0) \end{multline}$$ $$\begin{multline} y_0' = v_{y_0} \end{multline}$$ $$\begin{multline} v_{y_0}' = -b_0 v_{y_0} + k (y_\text{kursor} - y_0) + A \sin(\omega t) \end{multline}$$Uwzględniając warunki początkowe (wartości początkowe) dla sześciu zmiennych, możemy rozwiązać te równania różniczkowe, aby zobaczyć ewolucję układu w czasie.
Jednostki miary
Symulacje myPhysicsLab nie mają określonych jednostek miary, takich jak metry, kilogramy, sekundy. Jednostki są bezwymiarowe, mogą być interpretowane, jak chcesz, ale muszą być spójne w symulacji.
Na przykład, jeśli traktujemy jednostkę odległości jako jeden metr i jednostkę czasu jako jedną sekundę, to jednostka prędkości musi wynosić jeden metr/sekundę.
Dostosuj i udostępnij
Istnieje kilka sposobów na odtworzenie określonej konfiguracji eksperymentalnej. Najłatwiej jest kliknąć przycisk „udostępnij”.
- Zmodyfikuj symulację, zmieniając parametry, takie jak grawitacja, tłumienie oraz przeciągając obiekty za pomocą myszy.
- Kliknij przycisk „udostępnij”. Skopiuj adres URL z okna dialogowego.
- Udostępnij adres URL lub zapisz go w pliku tekstowym do późniejszego wykorzystania.
Gdy odbiorca kliknie adres URL, EasyScript osadzony w tym adresie powieli warunki, które zostały ustawione.
Zobacz Dostosowywanie symulacji myPhysicsLab (en) jak dodatkowo programować symulacje z bezpośrednim wykorzystaniem JavaScript lub EasyScript.