Podwójna sprężyna 2D


Symulacja pokazuje dwa obiekty połączone sprężynami i zawieszone w punkcie kotwiczenia. Obiekty mogą poruszać się w 2 wymiarach i działa grawitacja. Punkt kotwiczenia jest ruchomy.

Można przeciągnąć dowolną masę za pomocą myszy. Można także przeciągnąć górny punkt kotwiczenia. Kliknij przycisk „stan spoczynku”, aby ustawić masy w równowadze spoczynkowej. Spróbuj zmienić parametry, takie jak grawitacja, masa, sztywność sprężyny i opory (tłumienie).

Zależności matematyczne użyte w symulacji są pokazane poniżej. Zagadnienia programistyczne patrz strona źródłowa (en).

pokaż/ukryj opis

Fizyka

Podwójna sprężyna z dwoma obciążnikami, zaczepiona w nieruchomym (ale przeciągalnym) punkcie kotwiczącym, kołysze się w dwóch wymiarach. Ciężarki traktujemy jako punkty materialne. Wielkości dotyczące górnej sprężyny i obciążnika oznaczamy indeksem 1, a dolnej sprężyny i obciążnika indeksem 2.




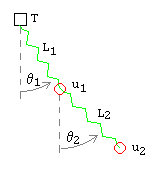
podwójna sprężyna 2D
zmienne

Określamy następujące zmienne:

  • θ = kąt ( 0= pion)
  • S = odkształcenie sprężyny (przemieszczenie od długości spoczynkowej)
  • L = długość sprężyny
  • u = położenie ciężarka
  • v = u'= prędkość ciężarka
  • a = u''= przyspieszenie ciężarka
  • F = wypadkowa siła działająca na ciężarek

Wprowadzamy kilka stałych:

  • R = długość spoczynkowa sprężyny
  • T = położenie punktu kotwiczącego
  • m = masa ciężarka
  • k = współczynnik sprężystości sprężyny
  • b = stała tłumienia (oporu)
  • g = przyspieszenie grawitacyjne

Zauważ, że dla tej symulacji oś pionowa jest skierowana w dół.

Oto równania ruchu. Wyprowadzenie jest podobne do podanego dla pojedynczej sprężyny 2D.

F1x = m1 a1x = −k1 S1 sin θ1 − b1 v1x + k2 S2 sin θ2
F1y = m1 a1y = −k1 S1 cos θ1 − b1 v1y + k2 S2 cos θ2 + m1 g
F2x = m2 a2x = −k2 S2 sin θ2 − b2 v2x
F2y = m2 a2y = −k2 S2 cos θ2 − b2 v2y + m2 g

Odkształcenia sprężyn Sn i kąty θn zależą od położeń un ciężarków w następujący sposób:

L1 = √((u1x − Tx)2 + (u1y − Ty)2)
L2 = √((u2x − u1x)2 + (u2y − u1x)2)
S1 = L1 − R1
S2 = L2 − R2
cos θ1 = (u1y − Ty)/L1
sin θ1 = (u1x − Tx)/L1
cos θ2 = (u2y − u1y)/L2
sin θ2 = (u2x − u1x)/L2

Rozwiązanie numeryczne

Aby rozwiązać te równania ruchu numerycznie, tak abyśmy mogli sterować symulacją, stosujemy metodę Rungego-Kutty rozwiązywania układów równań różniczkowych zwyczajnych. Musimy przekształcić cztery równania ruchu drugiego rzędu na osiem równań pierwszego rzędu.

u1x' = v1x
u1y' = v1y
u2x' = v2x
u2y' = v2y
v1x' = −(k1/m1) S1 sin θ1 − (b1/m1) v1x + (k2/m1) S2 sin θ2
v1y' = −(k1/m1) S1 cos θ1 − (b1/m1) v1y + (k2/m1) S2 cos θ2 + g
v2x' = −(k2/m2) S2 sin θ2 − (b2/m2) v2x
v2y' = −(k2/m2) S2 cos θ2 − (b2/m2) v2y + g

Należy pamiętać, że odkształcenia sprężyn Sn i kąty θn są funkcjami położeń ciężarków un jak to podano wcześniej.

Jednostki miary

Symulacje myPhysicsLab nie mają określonych jednostek miary, takich jak metry, kilogramy, sekundy. Jednostki są bezwymiarowe, mogą być interpretowane, jak chcesz, ale muszą być spójne w symulacji.

Na przykład, jeśli traktujemy jednostkę odległości jako jeden metr i jednostkę czasu jako jedną sekundę, to jednostka prędkości musi wynosić jeden metr/sekundę.

Dostosuj i udostępnij

Istnieje kilka sposobów na odtworzenie określonej konfiguracji eksperymentalnej. Najłatwiej jest kliknąć przycisk „udostępnij”.

  1. Zmodyfikuj symulację, zmieniając parametry, takie jak grawitacja, tłumienie oraz przeciągając obiekty za pomocą myszy.
  2. Kliknij przycisk „udostępnij”. Skopiuj adres URL z okna dialogowego.
  3. Udostępnij adres URL lub zapisz go w pliku tekstowym do późniejszego wykorzystania.

Gdy odbiorca kliknie adres URL, EasyScript osadzony w tym adresie powieli warunki, które zostały ustawione.

Zobacz Dostosowywanie symulacji myPhysicsLab (en) jak dodatkowo programować symulacje z bezpośrednim wykorzystaniem JavaScript lub EasyScript.

Opublikowano po raz pierwszy w kwietniu 2001 roku.

Źródło: