Spróbuj zmienić układ klocków, aby opierały się o siebie pod różnymi kątami lub układaj jeden na drugim. Zobaczysz, że są bardzo śliskie i ciężko jest ułożyć stos! Wynika to z faktu, że w tej symulacji nie występuje tarcie kontaktowe.
Siły kontaktowe są pokazane jako czerwone linie, które pojawiają się w rogach obiektów. Siły kontaktowe występują w parach (równe co do wartości i przeciwnie skierowane), ale tutaj pokazano tylko jedną z każdej pary.
Informacje na temat tarcia i tłumienia: w tej symulacji na styku między obiektami nie występuje żadne tarcie, dzięki czemu mogą łatwo przesuwać się względem siebie. Parametr tłumienia, który można zmodyfikować, ma związek z ruchem obiektów w przestrzeni -- przyjmujemy, że obiekty poruszają się w ośrodku lepkim.
Jak obliczyć siły kontaktowe – przegląd
Może cię zaskoczyć, że umieszczenie spoczywających przedmiotów na podłodze to bardzo trudny problem!
Jest tak dlatego, że siły kontaktowe są trudne do wyrażenia. Inne siły są znacznie prostsze, ponieważ zależą tylko od położenia jednego lub dwóch obiektów. Na przykład siła działania sprężyny między dwoma przedmiotami zależy tylko od położenia punktów końcowych sprężyny. Ale siły kontaktowe między obiektami zależą w dość złożony sposób od wszystkich pozostałych sił działających na te obiekty i tego, w jaki sposób stykają się ze sobą.
Opisane tutaj oprogramowanie (klasa o nazwie ContactSim) do obliczania sił kontaktowych ściśle współpracuje z oprogramowaniem, które obsługuje zderzenia, patrz Bryła sztywna - zderzenia. To oprogramowanie (nadklasa o nazwie ImpulseSim) zajmuje się kolizjami. W rezultacie nie powinno dojść do zderzenia, gdy kod siły nacisku jest aktywny, ponieważ kod zderzenia wykrywa kolizje, cofa się w czasie tuż przed i przykłada odpowiedni impuls, powodujący odbijanie się obiektów (zmienia zwroty ich prędkości). Nadklasa oblicza również wpływ działających na obiekty sił zewnętrznych, takich jak siły grawitacyjne, ciągu, sprężystści i tłumienia. (Co ciekawe, to te siły zewnętrzne powodują pojawienie się sił kontaktowych: bez nich nie byłoby sił popychających obiekty do siebie.)
Chodzi o to, aby obliczyć dokładną siłę potrzebną przy każdym zetknięciu, aby
tylko zapobiec przenikaniu się obiektów. Siły te są obliczane
w metodzie ewaluacji klasy ContactSim, która jest
wielokrotnie wywoływana przez układ rozwiązywania równań różniczkowychw celu znalezienia przyspieszeń
obiektów. Solver równania różniczkowego wykorzystuje te informacje do postępu stanu
układu w czasie. Na wstępie tej metody ewaluacji mamy dane
aktualne pozycje i prędkości każdego obiektu, co jest niezbędne do ustalenia,
gdzie znajdują się punkty styku i geometrii sił kontaktowych między
obiektami.
Najpierw znajdujemy wszystkie kontakty spoczynkowe między obiektami. Kryteria są następujące: róg musi znajdować się bardzo blisko krawędzi i poruszać się bardzo powoli (w kierunku prostopadłym do krawędzi). Korzystając z tych kryteriów, tworzymy listę punktów kontaktowych. Dla każdego styku gromadzimy informacje, takie jak: które dwa obiekty są w kontakcie, jaka jest normalna (wektor prostopadły) do krawędzi, jak się ma punkt styku do każdego obiektu itp.
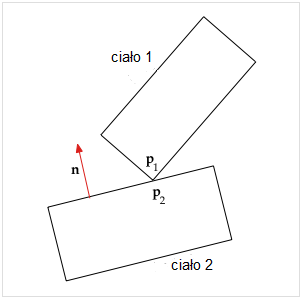
2 stykające się ciała
Rozważmy dwa stykające się obiekty przedstawione na rysunku. Punkt kontaktowy ciała 1 to wierzchołek oznaczony p1 , punkt kontaktowy ciała 2 znajduje się na krawędzi i jest oznaczony p2 . Niech d będzie odległością między dwoma punktami, tak że d = |p1 − p2| . Niech n będzie wektorem normalnym wskazującym na zewnątrz ciała 2 (prostopadłym do jego krawędzi). Na schemacie poniżej widzimy dwie siły wzajemnego działania, przyłożone w punkcie styku. Siła kontaktowa f n działa na ciało 1, zapobiegając jego przenikaniu do ciała 2. Zgodnie z trzecią zasadą dynamiki Newtona działa także (równa co do wartości, ale o przeciwnym zwrocie) siła −f n, przyłożona do ciała 2, zapobiegająca jego przenikaniu do ciała 1.
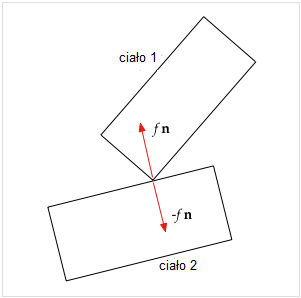
2 ciała z siłami kontaktowymi
Chcemy znaleźć (obecnie nieznane) siły kontaktowe, takie jak f n ,które ledwo powstrzymają obiekty przed przyspieszaniem do siebie, przeciwdziałając wszystkim innym siłom (takim jak grawitacja), które mają tendencję do zsuwania obiektów razem.
Koncentrujemy się na odległości kontaktowej d , odstępie między punktami kontaktu. Ponieważ przedmioty stykają się, to d = 0 (w granicach tolerancji numerycznej). Wartość d < 0 wskazywałaby, że obiekty się przenikają. Wartość d > 0 wskazywałaby, że obiekty nie stykają się, lecz są oddzielone odległością d .
Szybkość zmiany odległości kontaktowej jest prędkością d' . Ponieważ obiekty są w kontakcie spoczynkowym, mamy d' = 0 (w granicach tolerancji numerycznej). Było to jedno z kryteriów wyboru zestawu spoczynkowych punktów kontaktowych. Zauważ, że obiekty mogą się przesuwać względem siebie, ponieważ istotny dla nas jest tylko ruch w kierunku normalnym (prostopadłym do krawędzi).
Najbardziej interesuje nas d'' , przyspieszenie szczeliny. Bez sił kontaktowych stwierdzimy, że dla większości punktów kontaktowych d'' < 0, co oznacza, że obiekty wpadając na siebie, będą się przenikały.
Obliczanie sił kontaktowych jest dość trudne, ponieważ wszystkie są ze sobą powiązane. Jest tak, ponieważ możemy mieć złożony układ obiektów spoczywających na sobie. Rozwiązanie polega na znalezieniu zestawu równań, które dokładnie odzwierciedlają wpływ każdej siły nacisku na każdą szczelinę. Następnie rozwiązujemy równania, aby znaleźć siły, które dokładnie ustawiają d'' = 0 w każdym punkcie styku. W rzeczywistości dopuszczamy również wartość d'' > 0, co oznacza, że obiekty się rozdzielają, a zatem nie ma siły nacisku na tym konkretnym styku.
Po znalezieniu dokładnych sił na każdym styku, zachowujących kontakty spoczynkowe (zapobiegających przyspieszaniu obiektów w siebie), przykładamy teraz te siły do każdego obiektu. Powoduje to zmianę ich przyspieszeń. Uwzględniamy to w solverze równań różniczkowych, który rozwija ewolucję symulacji w czasie przy użyciu tych nowych przyspieszeń. Ale teraz te przyspieszenia są modyfikowane tak, aby obiekty pozostały w kontakcie spoczynkowym, zgodnie z potrzebami.
Obliczanie sił kontaktowych - szczegółowo
Ten program do obliczania sił kontaktowych nazywa się ContactSim; jest
jest to podklasa klasy ImpulseSim, opisanej na stronie
Bryła sztywna - zderzenia.
To co poniżej opiera się na tych wyjaśnieniach.
Zastosowane tutaj algorytmy oparte są na dwóch artykułach autorstwa Davida Baraffa:
- [Baraff-1] David Baraff, An Introduction to Physically Based Modeling: Rigid Body Simulation II - Nonpenetration Constraints. Są to notatki z wykładu z Physically Based Modeling: Principles and Practice (Online Siggraph '97 Course Notes). Zauważ, że na stronie D62 występuje błąd typograficzny: w kilku miejscach, w których widzisz "a force of j nj(t0)", powinno być "a force of fj nj(t0)".
- [Baraff-2] David Baraff. Fast contact force computation for nonpenetrating rigid bodies. Computer Graphics Proceedings, Annual Conference Series: 23-34, 1994. 12 pages.
Zobacz także Wahadło - siły reakcji, prostszy przykład obliczania sił kontaktowych za pomocą matematyki pokazanej na tej stronie.
Załóżmy, że mamy zestaw n kontaktów w określonej (ale dowolnej) kolejności. Definiujemy następujące zmienne:
- n = liczba kontaktów.
- di'' = przyspieszenie odległości kontaktowej i-tego kontaktu.
- a = n-elementowy wektor przyspieszeń odległości kontaktowych, taki że ai = di''
- f = n-elementowy wektor wartości sił kontaktowych (do ustalenia)
- b = n-elementowy wektor podający przyspieszenia odległości kontaktowych wynikające z działania sił zewnętrznych (grawitacja, siła ciągu, itp.).
- A = macierz n × n, która określa, w jaki sposób siły kontaktowe wpływają na przyspieszenie odległości kontaktowych
- ai j = element macierzy A w i-tym wierszu i j-tej kolumnie.
Naszym celem jest utworzenie i rozwiązanie (z zastrzeżeniem pewnych ograniczeń) równania macierzowego
| a = A f + b | (1) |
Wyraz ai j macierzy mówi, o ile zmieni się di'' z powodu jednostkowej zmiany fj. Jeśli wykonamy mnożenie macierzy w równaniu (1) zobaczymy, że przyspieszenie i-tej odległości kontaktowej jest dane przez
| di'' = ai 1 f1 + ai 2 f2 +. . . + ai j fj + . . . + ai n fn + bi | (2) |
To mówi, że przyspieszenie i -tej odległości kontaktowej jest funkcją sił kontaktowych f1, f2,..., fn i sił zewnętrznych w bi. Możemy ustalić ai j i bi (patrz poniżej). Wartości di'' muszą wychodzić zerowe lub dodatnie, ponieważ obiekty nie mogą przyspieszać do siebie (są to bryły sztywne, które się nie przenikają). Zatem jedynymi niewiadomymi są siły kontaktowe fi i możemy rozwiązać układ równań, aby je znaleźć.
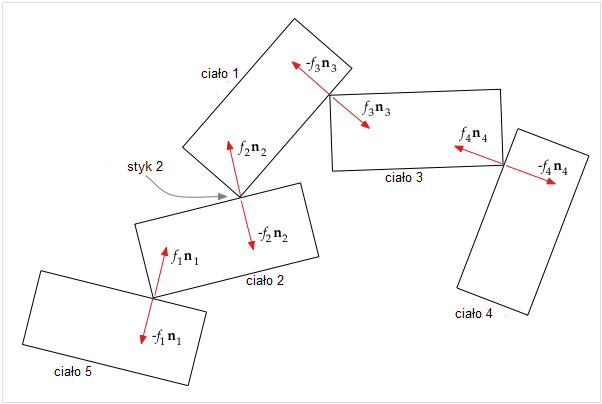
5 ciał, 4 punkty styku, 8 sił kontaktowych
Aby zilustrować sposób obliczania macierzy A i wektora b, rozważmy powyższy rysunek. Mamy tu 5 ciał, pozostających w kontakcie spoczynkowym w 4 punktach kontaktowych, oraz pokazano wypadkowe siły kontaktowe. (Zauważ, że wektory normalne ni są zawsze prostopadłe do krawędzi i zgodnie z konwencją skierowane na zewnątrz obiektu; to określa, które siły mają znaki minus). Punkty styku są ponumerowane zgodnie z siłami kontaktowymi, tak że siła f1 n1 działa w punkcie 1, itd. Skupiając się na styku 2 (między ciałami 1 i 2), z równania (2) możemy zapisać
| d2'' = a2,1 f1 + a2,2 f2 + a2,3 f3 + a2,4 f4 + b2 | (3) |
Zastanówmy się, co wpływa na przyspieszenie odległości kontaktowej d2''. Wszystko, co przyspiesza ciało 1 lub ciało 2, może wpływać na d2''. Oto lista tych źródeł przyspieszenia d2'' i gdzie występują w równaniu (3).
- Dla wszystkich sił nie-kontaktowych (grawitacja, ciąg itp.) działających obecnie na ciało 1, obliczamy, jakie jest wynikające z tego przyspieszenie narożnika ciała 1 na styku 2; uwzględnione to jest w b2 .
- Podobnie w przypadku wszystkich sił nie-kontaktowych (grawitacja, ciąg itp.) działających obecnie na ciało 2, obliczamy, jakie jest wynikające z tego przyspieszenie punktu ciała 2 na styku 2; uwzględnione to jest w b2 .
- W odniesieniu do siły kontaktowej f1 n1 , dla jednostkowej zmiany f1 obliczamy, jakie byłoby wynikające stąd przyspieszenie punktu ciała 2 na styku 2; uwzględnione to jest w a2,1 .
- W odniesieniu do siły kontaktowej f2 n2 , dla jednostkowej zmiany f2 obliczamy, jakie byłoby wynikające stąd przyspieszenie rogu ciała 1 na styku 2; uwzględnione to jest w a2,2 .
- W odniesieniu do siły kontaktowej −f2 n2 , dla jednostkowej zmiany f2 obliczamy, jakie byłoby wynikające stąd przyspieszenie punktu ciała 2 na styku 2; dołożone jest to do a2,2 .
- W odniesieniu do siły kontaktowej −f3 n3 , dla jednostkowej zmiany f3 obliczamy, jakie byłoby wynikające stąd przyspieszenie rogu ciała 1 na styku 2; uwzględnione to jest w a2,3 .
- Ponieważ siły kontaktowe f4 n4 i −f4 n4 nie wpływają bezpośrednio na ciała 1 lub 2, przyjmujemy a2,4 = 0 .
Mam nadzieję, że daje to pewne wyobrażenie tego, jak obliczana jest macierz A i wektor b. calculated. Szczegółowe informacje na temat tych obliczeń podano poniżej w sekcjach Obliczanie macierzy A i Obliczanie wektora b.
Po znalezieniu macierzy A i wektora b, jesteśmy gotowi do wyznaczenia z równania (1) nieznanych wielkości siły w wektorze f, z zastrzeżeniem następujących 3 ograniczeń:
| ai ≥ 0, fi ≥ 0, a · f = 0 | (4) |
Opisowo te ograniczenia oznaczają:
- ai ≥ 0 oznacza, że nie zezwalamy na przenikanie (które występuje, gdy ai < 0 ). Wymagamy, aby wszystkie względne normalne przyspieszenia między ciałami w punktach styku były zerowe (kontakt) lub dodatnie (rozdzielanie).
- fi ≥ 0 oznacza, że wymagamy sił kontaktowych równych zero lub dodatnich, ponieważ mogą one tylko naciskać, a nie ciągnąć.
- a · f = 0 oznacza, że w każdym punkcie styku, jeśli występuje siła kontaktowa, wówczas przyspieszenie wynosi zero LUB jeśli występuje przyspieszenie (przy rozdzieleniu), wówczas nie ma siły kontaktowej. Kropka w równaniu to iloczyn skalarny wektorów.
Artykuł Fast contact force computation for nonpenetrating rigid bodies. autorstwa Davida Baraffa szczegółowo opisuje sposób rozwiązywania równania (1) z zastrzeżeniem ograniczeń (4). Podam tutaj krótki opis działania algorytmu opisanego w tym dokumencie.
Algorytm rozpoczyna się od ustawienia wszystkich sił kontaktowych w f na zero. Podstawową ideą jest dokładanie jednej siły kontaktowej na raz, siły wystarczającej do zachowania ograniczeń i dostosowanie innych sił w razie potrzeby. Ignorujemy punkty styku, których jeszcze nie rozważaliśmy, stopniowo zwiększając zestaw punktów spełniających ograniczenia. Oto bardzo uproszczony szkic tego, jak to działa:
- Zaczynamy od rozważenia tylko styku 1, ignorując wszystkie inne punkty styku (które prawdopodobnie nie spełniają warunku ai ≥ 0 ). Obliczamy wielkość siły f1 w punkcie styku 1, która jest wystarczająca, aby a1 = 0 .
- Następnie dokładamy styk 2. Rozwiązujemy względem f2 , dostosowując f1 w razie potrzeby, aby nasze trzy ograniczenia były spełnione dla a1, a2 i f1, f2 .
- Kontynuujemy dodawanie styków i sił kontaktowych pojedynczo, jednocześnie dostosowując poprzednie siły tak, aby zachować trzy ograniczenia równania (4).
W każdym punkcie rozwiązujemy podzbiór równania macierzowego (1) obejmujący tylko te punkty styku, które rozważaliśmy do tej pory. W ostatnim kroku dodaliśmy wszystkie punkty styku i dlatego mamy kompletne rozwiązanie równania (1) , które spełnia ograniczenia równania (4).
Teraz, gdy znamy siły kontaktowe, ostatnim krokiem jest przyłożenie ich do ciał,
co daje końcowy zestaw przyspieszeń ciał, które następnie oprogramowanie obliczeniowe
zwraca do solvera równania różniczkowego. W grę wchodzi tu układ powiązań,
w którym każda siła kontaktowa jest przyłożona do każdego ciała, aby określić, jak ta siła kontaktowa
wpływa na przyspieszenie liniowe i kątowe danego ciała. Proces ten jest bardzo
podobny do tego opisanego na stronie Bryła sztywna - zderzenia
dotyczącego traktowania sił takich jak
siły ciągu.
Solver równania różniczkowego następnie rozwija ewolucję symulacji w czasie, wykorzystując te nowe przyspieszenia. Przyspieszenia te zostały jednak dokładnie obliczone, aby ciała będące w kontakcie spoczynkowym pozostawały w kontakcie spoczynkowym bez wzajemnego przenikania.
Obliczanie macierzy A
Naszym celem tutaj jest obliczenie elementów macierzy A równania (1). Jak opisano powyżej, element o wskaźnikach i, j macierzy A, ai j, określa, w jaki sposób j-ta siła kontaktowa, fj, wpływa na przyspieszenie i-tej odległości kontaktowej, di''.
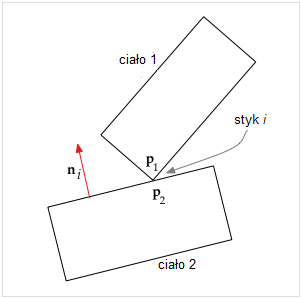
2 stykające się ciała
Dla konkretnego punktu styku i , niech ciała będą ponumerowane 1 i 2, przy czym ciało 2 określa wektor normalny ni skierowany od ciała 2 w kierunku ciała 1 (jak na schemacie powyżej). Niech p1 będzie punktem ciała 1, który styka się z punktem p2 ciała 2. Niech di będzie odległością między p1 i p2 . Jeśli potraktujemy p1 i p2 jako wektory o początkach w początku układu współrzędnych i końcach w tych punktach ciał 1 i 2, to ich różnica (p1 − p2) jest również wektorem i możemy zapisać
| di = ni ⋅ (p1 − p2) | (5) |
ponieważ iloczyn skalarny z normalną daje nam wartość składowej wektora (p1 − p2) w kierunku n . Zauważ, że di jest zatem wielkością skalarną. Pamiętając, że wszystkie zmienne w równaniu (5) są funkcjami czasu, możemy dwukrotnie zróżniczkować jak następuje:
di' = ni' ⋅ (p1 − p2) + ni ⋅ (p1' − p2')
di'' = ni'' ⋅ (p1 − p2) + 2 ni' ⋅ (p1' − p2')
+ ni ⋅ (p1'' − p2'')
Ponieważ jest to punkt styku, mamy, że p1 − p2 = 0 więc powyższe upraszcza się do
| di'' = ni ⋅ (p1'' − p2'') + 2 ni' ⋅ (p1' − p2') | (6) |
Drugi człon, 2 ni' ⋅ (p1' − p2') , jest zależny od prędkości (dzięki czemu można od razu go obliczyć, bez znajomości działających sił), i dlatego jest częścią bi . Zobacz Obliczanie wektora b poniżej. Zatem zależną od fj częścią równania (6) jest tylko
| ni ⋅ (p1'' − p2''). | (7) |
Siła kontaktowa fj nj tylko wtedy wpływa na di'', , jeśli działa na ciało 1 lub ciało 2. Jeśli tak nie jest, wiemy, że ai j = 0 . Załóżmy teraz, że fj nj wpływa na ciało 1 lub 2. Należy jednak pamiętać, że fj nj może być siłą kontaktową, która nie jest w i -tym punkcie styku (patrz na przykład wcześniejszy schemat 5 stykających się ciał). Możemy znaleźć ai j z geometrii sytuacji w sposób opisany poniżej.
Niech nj będzie wektorem normalnym w j -tym punkcie styku. Załóżmy, że j -ty kontakt dotyczy ciała 1. Wtedy siła kontaktowa wynosi fj nj jeśli punkt styku to narożnik ciała 1 lub −fj nj jeśli to krawędź. Z geometrii możemy obliczyć wpływ siły na ciało 1, i stąd na przyspieszenie p1'' . Jeśli kontakt dotyczy ciała 2, wtedy wpływa na p2'' . Następnie za pomocą równania (7) dojdziemy do wpływu fj nj na ai j .
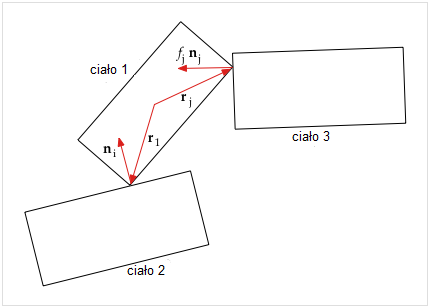
3 stykające się ciała
Zdefiniujmy następujące dodatkowe zmienne:
- x1 = środek masy ciała 1
- r1 = wektor od środka masy ciała 1 do p1 w i-tym punkcie styku
- rj = wektor od środka masy ciała 1 do j-tego punktu styku
- ω1 = wartość prędkości kątowej ciała 1
- ω1 = prędkość kątowa ciała 1, wektor, który jest prostopadły do płaszczyzny, czyli ω1 = {0, 0, ω1}.
- v1 = x1' = wektor prędkości środka masy ciała 1
- m1 = masa ciała 1
Wówczas p1 = x1 + r1 i uwzględniając, że wszystkie te zmienne są funkcjami czasu, możemy policzyć pochodne:
| p1' = x1' + r1' = v1 + ω1 × r1 | (7a) |
Wykorzystaliśmy tutaj fakt, że r1 zmienia się tylko przez obrót o prędkości ω1 . Elementarne prawa rachunku różniczkowego dają następnie wynik r1' = ω1 × r1 gdzie × oznacza iloczyn wektorowy. Obliczamy następną pochodną:
p1'' = v1' + ω1' × r1 + ω1 × r1'
| p1'' = v1' + ω1' × r1 + ω1 × (ω1 × r1) | (8) |
Człon ω1 × (ω1 × r1) jest zależny od prędkości, więc przechodzi do wektora b . Zatem zależna od fj część p1'' to
| v1' + ω1' × r1 | (8a) |
Naszym zadaniem jest teraz zbadanie, jak bardzo wpływa na to jednostkowa zmiana fj .
Ponieważ v1' jest przyspieszeniem liniowym ciała 1, z pierwszej zasady dynamiki Newtona mamy
v1' = (wypadkowa siła działająca na ciało 1) /m1
Dlatego część v1' zależna od fj to
fj nj /m1
Ponieważ pracujemy w 2D, możemy zapisać przyspieszenie kątowe jako
ω1' = τ1 / I1
gdzie τ1 = moment obrotowy działający na ciało 1, a I1 = moment bezwładności ciała 1 wokół środka masy. (W 3D, przyspieszenie kątowe jest inaczej określone; zobacz [Baraff-1] po więcej informacji). Przypuśćmy, że j -ty kontakt następuje w punkcie pj , a wektor rj ma początek w środku masy obiektu 1, a koniec w pj . Wówczas moment siły fj nj wynosi rj × fj nj . Czyli zależna od fj część ω1' to
(rj × fj nj) / I1
i możemy zapisać równanie (8a), zależną od fj część p1'' , w postaci
fj nj / m1 + (rj × fj nj) × r1 / I1
= fj (nj / m1 + (rj × nj) × r1 / I1),
a zależną od fj część di'' w równaniu (6) jako
fj ni ⋅ (nj / m1 + (rj × nj) × r1 / I1)
Dlatego patrząc wstecz na równanie (2) dla kontekstu, mamy zależność di'' od fj jako
| ni ⋅ (nj / m1 + (rj × nj) × r1 / I1) | (9) |
co wchodzi do ai j .
Należy pamiętać, że przyjęliśmy, że fj nj działa na ciało 1. Jeśli zamiast tego −fj nj działa na ciało 1, to zmienia to znak wyrażenia (9). Jeśli fj nj działa na ciało 2, a nie na 1, wtedy wpływa na p2'' w równaniu (6), więc jest zmiana znaku i także używamy m2, r2 i I2 w wyrażeniu (9), a rj jest obliczane w odniesieniu do ciała 2. Również w przypadku, gdy fj nj jest się w punkcie styku ciał 1 i 2, wtedy fj nj działa na ciało 1, a −fj nj działa na ciało 2 i kończymy używając wyrażenia (9) dwa razy i umieszczając sumę w ai j .
Obliczanie wektora b
Tutaj obliczamy wektor b z równania (1). Wektor b określa, jakie byłoby przyspieszenie odległości styku di'' przy braku sił kontaktowych. Zależy to od sił nie-kontaktowych, takich jak grawitacja, ciąg, siła sprężyny, tłumienie itp., ale ma również składnik zależny od prędkości.
Zauważ, że to te siły powodują istnienie sił kontaktowych; siły kontaktowe pojawiają się w reakcji na inne siły, które popychają obiekty do siebie, stąd są również znane jako „siły reakcji”.
W kontekście rozwiązywania równania (1), wektor b jest uważany za wektor „stały”, ponieważ w chwili, gdy rozwiązujemy równanie (1) dla sił kontaktowych, wektor b jest znaną wielkością.

2 stykające się ciała
Kontynuujemy ten sam scenariusz i używamy zmiennych zdefiniowanych w poprzedniej części Obliczanie macierzy A. To znaczy, bierzemy pod uwagę i-ty styk i numerujemy ciała jako 1 i 2, gdzie ciało 2 określa wektor normalny ni styku. Szukamy wyrażenia bi w równaniu (2). Zaczynamy od równania (6), które zostało wyprowadzone w poprzedniej części:
di'' = ni ⋅ (p1'' − p2'') + 2 ni' ⋅ (p1' − p2')
Najpierw rozważamy wyrażenie 2 ni'⋅ (p1' - p2'). Jest zależne tylko od aktualnej prędkości, a nie od przyspieszenia, a zatem jest niezależne od przyłożonych sił kontaktowych i dlatego należy do wektora b. Przypomnijmy, że ni to wektor normalny do powierzchni ciała 2. Dlatego, jeśli ciało 2 jest nieruchome (na przykład ściana lub podłoga), wówczas normalna nie zmienia się, więc ni' jest wektorem zerowym, a to wyrażenie wynosi zero.
Wyprowadzenie ni '
Przypomnijmy, że ni jest wektorem normalnym do ciała 2, zgodnie z wcześniejszymi ustaleniami. Wiemy, że ciało 2 obraca się z prędkością kątową ω2 . Dlatego, wykorzystując elementarne wzory rachunku różniczkowego, możemy zapisać
ni' = ω2 × ni
gdzie traktujemy prędkość kątową jako wektor ω2 prostopadły do płaszczyzny, tak że
ω2 = {0, 0, ω2}
Oto wyprowadzenie tego wyniku: Niech ni będzie zdefiniowane w następujący sposób (ponieważ jesteśmy w 2D, współrzędna z wynosi zero):
ni = {nix, niy, 0}
Wiemy, że wektor ni obraca się z prędkością ω2 . Ignorując jakiekolwiek przyspieszenie, moglibyśmy zapisać wektor ni jako funkcję czasu w ten sposób:
ni = |ni| {cos(ω2 t), sin(ω2 t), 0}
Gdzie |ni| jest wartością wektora ni , a t = czas. Pierwsza pochodna wynosi wtedy
ni' = |ni| {−ω2 sin(ω2 t), ω2 cos(ω2 t), 0}
co jest równoważne z:
ni' = {−ω2 niy, ω2 nix, 0}
i co można również wyrazić jako iloczyn wektorowy dwóch wektorów:
ni' = ω2 × ni
Teraz możemy użyć tego wyrażenia dla ni' i równania (7a), co daje wyrażenie dla p1' (i również podobnie dla p2' ) do napisania tego
| 2 ni' ⋅ (p1' − p2') = 2 (ω2 × ni) ⋅ (v1 + ω1 × r1 − (v2 + ω2 × r2)) | (10) |
Powyższe wyrażenie jest częścią równania (6) i dodaje się do bi . Ale tylko w przypadku, gdy ciało 2 jest obiektem poruszającym się; jeżeli ciało 2 jest nieruchome (na przykład ściana lub podłoga), to ni' wynosi zero.
Następnie rozważmy wyrażenie ni ⋅ (p1'' − p2'') równania (6). Musimy uwzględnić w bi wpływ wszelkich sił nie-kontaktowych na przyspieszenia punktów styku p1 i p2 . Zaczniemy od równania (8), które zostało wyprowadzone w poprzedniej części:
p1'' = v1' + ω1' × r1 + ω1 × (ω1 × r1)
Okazuje się, że przyspieszenia
v1'
i
ω1'
, które są spowodowane
siłami nie-kontaktowymi, zostały już dla nas obliczone przez wcześniejsze procesy (patrz
metoda ewaluacji klasy ImpulseSim). Te przyspieszenia są
przekazywane do naszej metody ewaluacji, więc po prostu wstawiamy je do równania
(8), aby uzyskać
p1''
(a
p2''
ma podobne wyrażenie). Możemy więc zapisać
to jako
| ni ⋅ (p1'' − p2'') = ni ⋅ (v1' + ω1' × r1 + ω1 × (ω1 × r1) − (v2' + ω2' × r2 + ω2 × (ω2 × r2))) | (11) |
co jest częścią równania (6), którą należy dodać do bi . Należy pamiętać, że w powyższym równaniu, v1' i ω1' są przyspieszeniami ciała 1 spowodowanymi jedynie siłami nie-kontaktowymi (i podobnie dla v2' i ω2' ).
Mamy teraz w wyrażeniach (10) i (11), niezależne od siły nacisku części równania (6), które wchodzą do bi .
Jednostki miary
Symulacje myPhysicsLab nie mają określonych jednostek miary, takich jak metry, kilogramy, sekundy. Jednostki są bezwymiarowe, mogą być interpretowane, jak chcesz, ale muszą być spójne w symulacji.
Na przykład, jeśli traktujemy jednostkę odległości jako jeden metr i jednostkę czasu jako jedną sekundę, to jednostka prędkości musi wynosić jeden metr/sekundę.
Dostosuj i udostępnij
Istnieje kilka sposobów na odtworzenie określonej konfiguracji eksperymentalnej. Najłatwiej jest kliknąć przycisk „udostępnij”.
- Zmodyfikuj symulację, zmieniając parametry, takie jak grawitacja, tłumienie oraz przeciągając obiekty za pomocą myszy.
- Kliknij przycisk „udostępnij”. Skopiuj adres URL z okna dialogowego.
- Udostępnij adres URL lub zapisz go w pliku tekstowym do późniejszego wykorzystania.
Gdy odbiorca kliknie adres URL, EasyScript osadzony w tym adresie powieli warunki, które zostały ustawione.
Zobacz Dostosowywanie symulacji myPhysicsLab (en) jak dodatkowo programować symulacje z bezpośrednim wykorzystaniem JavaScript lub EasyScript.
Opublikowano po raz pierwszy w styczniu 2007 roku.