Jeśli pobawisz się pokazaną powyżej symulacją, zauważysz, że może ona łatwo "zawiesić się", co oznacza, że obiekty nakładają się na siebie. Paragraf poniżej na temat Kolizji spoczynkowej wyjaśnia, dlaczego tak się dzieje.
Oto obraz rozmieszczenia elementów sterujących klawiatury. Jeśli klawisze nie działają, spróbuj najpierw kliknąć w pobliżu obiektu - spowoduje to, że naciśnięcia klawiszy będą przekazywane do symulacji.
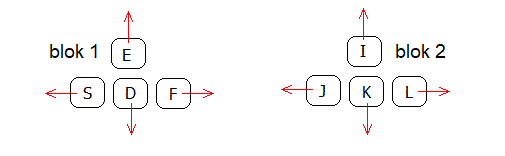
sterowanie ciągiem za pomocą klawiatury
Wykres słupkowy energii
Kliknij pole wyboru „pokaż energię”, aby zobaczyć wykres słupkowy pokazujący energię potencjalną oraz kinetyczną ruchu obrotowego i postępowego.
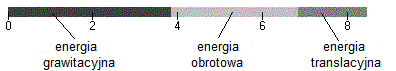
wykres słupkowy energii
Aby sprawdzić poprawność symulacji, spójrz na energię przed i po zderzeniu. Jeśli tłumienie = 0, a współczynnik restytucji = 1, energia nie powinna się zmienić.
Zobacz paragraf Energia i pęd, aby dowiedzieć się, jak te wielkości są obliczane.
Wykrywanie kolizji
Wyjaśnienia tutaj opierają się na tych podanych na stronie Bryła sztywna - siły. W szczególności nazwy zmiennych przedstawiono w paragrafie Opis fizyczny ruchu bryły sztywnej.
Na każdym etapie symulacji sprawdzamy, czy występuje kolizja. Ciała mogą zderzać się ze sobą lub ze ścianą graniczną. W przypadku prostokątnych kształtów, których używamy, prosta geometria pozwala ustalić, czy doszło do kolizji - sprawdzamy, czy jakikolwiek wierzchołek znajduje się w ścianie lub w ciele obcym.
Po wykryciu kolizji używamy wyszukiwania binarnego, aby cofnąć symulację do wcześniejszego stanu na krótko przed wystąpieniem kolizji. Następnie dokonujemy oszacowania momentu zderzenia i obliczamy wynikające z tego zmiany prędkości, jak opisano poniżej. Symulacja Zderzające się bloki dodatkowo opisuje te aspekty obsługi kolizji.
Fizyka zderzeń brył sztywnych w 2 wymiarach
Obsługa kolizji jest najtrudniejszą częścią tej symulacji. Wyjaśnienie tutaj jest dość zwięzłe, więc możesz również przeczytać inne opisy.
- Informacje o dynamice bryły sztywnej Chrisa Heckera. Zobacz zwłaszcza jego artykuł w Game Developer Magazine Collision Response. Łatwy do czytania, z wieloma innymi odnośnikami wymienionymi na stronie internetowej. Niestety niektóre dokumenty PDF nie drukują poprawnie wyrażeń matematycznych.
- Physically Based Modeling to zbiór notatek kursowych z Siggraph '97 Andrew Witkin i David Baraff. Zobacz szczególnie paragrafy dotyczące dynamiki bryły sztywnej. Dość kompletne i rygorystyczne wyjaśnienia, ale wciąż dość czytelne. Obejmuje przypadek trójwymiarowy, a także siły kolizji spoczynkowej.
- Fizyka dla programistów gier David M. Bourg (Helion).
- Podręcznik Engineering Mechanics Dynamics Roberta Soutas-Little i Daniela Inmana.
- Praca magisterska Wykrywanie i rozwiązywanie kolizji ciał sprężystych w dwuwymiarowych symulacjach komputerowych Andrzeja Surdeja.
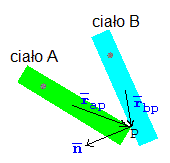
wektory związane z kolizją
Załóżmy, że wierzchołek ciała A zderza się z krawędzią ciała B w punkcie P. Wprowadzamy następujące zmienne
- ma, mb = masy ciał A, B
- rap = wektor od środka masy ciała A do punktu P
- rbp = wektor od środka masy ciała B do punktu P
- ωa1, ωb1 = początkowe (przed zderzeniem) prędkości kątowe ciał A, B
- ωa2, ωb2 = końcowe (po zderzeniu) prędkości kątowe ciał A, B
- va1, vb1 = początkowe (przed zderzeniem) prędkości środków mas ciał A, B
- va2, vb2 = końcowe (po zderzeniu) prędkości środków mas ciał A, B
- vap1 = początkowa prędkość (przed zderzeniem) punktu uderzenia w ciało A
- vbp1 = początkowa prędkość (przed zderzeniem) punktu uderzenia w ciało B
- n = wektor normalny (prostopadły) do krawędzi ciała B
- e = współczynnik restytucji (0 = doskonale niesprężyste, 1 = doskonale sprężyste)
Teraz używamy standardowego wzoru na prędkość dowolnego punktu bryły sztywnej poruszającej się ruchem postępowym i obrotowym, aby uzyskać prędkości przed zderzeniem punktów kolizyjnych (punkt P na każdym ciele).
vap1 = va1 + ωa1 × rap
vbp1 = vb1 + ωb1 × rbp
Podobnie mamy końcowe prędkości po zderzeniu vap2 i vbp2 jako
vap2 = va2 + ωa2 × rap
vbp2 = vb2 + ωb2 × rbp
Tutaj rozważamy prędkość kątową jako trójwymiarowy wektor prostopadły do płaszczyzny, tak że iloczyn wektorowy jest obliczany jako
ω × r = (0, 0, ω) × (rx, ry, 0) = (−ω ry, ω rx, 0)
Teraz możemy znaleźć wyrażenie określające prędkośći, z jaką zbliżają się do siebie punkty kolizji. Nazywamy to prędkością względną. Niech vab1 będzie początkową (przed zderzeniem) prędkością względną, a vab2 będzie końcową (po zderzeniu) prędkością względną. Prędkości względne definiujemy w następujący sposób
vab1 = vap1 − vbp1
vab2 = vap2 − vbp2
Korzystając z podanych wyżej wzorów prędkości punktu bryły sztywnej, możemy je rozszerzyć do postaci
| vab1 = va1 + ωa1 × rap − vb1 − ωb1 × rbp | (4) |
| vab2 = va2 + ωa2 × rap − vb2 − ωb2 × rbp | (5) |
Niech n będzie wektorem normalnym (prostopadłym) do uderzanej krawędzi ciała B, skierowanym na zewnątrz ciała B o długości 1. Teraz możemy znaleźć prędkość względną w kierunku normalnej n wykorzystując iloczyn skalarny wektorów:
względna prędkość normalna = vab1 · n
Zauważ, że aby doszło do kolizji, ta względna prędkość normalna musi być "ujemna" (tzn. obiekty muszą się do siebie zbliżać). Niech e będzie współczynnikiem restytucji zderzenia, zawierającym się między 0 (całkowicie niesprężyste) i 1 (idealnie sprężyste). Dokonujemy teraz ważnego założenia w postaci następującego związku
| vab2 · n = −e vab1 · n | (6) |
Mówi to, że prędkość, z jaką obiekty odskakują, jest proporcjonalna do prędkości, z jaką się zbliżają. Współczynnikiem proporcjonalności jest współczynnik restytucji e .
Popęd siły w zderzeniu
Aby rozwiązać kolizję, wykorzystamy pojęcie popędu. Popęd siły (impuls) jest równy zmianie pędu ciała. Podczas zderzenia przez bardzo krótki czas działa bardzo duża siła. Jeśli scałkujemy tę siłę po tym krótkim czasie, otrzymamy popęd.
Dlaczego potrzebujemy tej dziwnej koncepcji impulsu? Dlaczego nie użyć po prostu znanej koncepcji siły, jak w F = m a ? Odpowiedź jest taka, że nie wiemy, jakie są siły podczas zderzenia. Za pomocą superkomputera i bardzo złożonego oprogramowania możemy modelować siły występujące podczas zderzenia. Musielibyśmy znać szczegóły dotyczące materiałów ciał, ich dokładnej geometrii, jak odkształcają się pod wpływem naprężeń, jak naprężenie rozprzestrzenia się w ciele itp.
To znacznie wykracza poza naszą prostą symulację. Na szczęście możemy założyć, że kolizja następuje w tak krótkim czasie, że położenie i orientacja ciał nie zmienia się. Natomiast jedyne, co się zmienia, to prędkości ciał. Ponieważ zmiana prędkości jest zmianą pędu (pamiętaj, że pęd = prędkość razy masa), dochodzimy do pojęcia popędu.
Zakładamy brak tarcia przy zderzeniu, więc jedyna siła działająca podczas zderzenia ma kierunek prostopadły do krawędzi, dany przez wektor n . (Tarcie skutkuje działaniem również siły równoległej do krawędzi). Niech całkowity popęd powstały przy zderzeniu będzie j n gdzie j jest parametrem (wartość popędu) do ustalenia. Ciało A doświadcza impulsu j n podczas gdy ciało B doświadcza równego co do wartości, ale o przeciwnym zwrocie impulsu −j n . Impuls jest równy zmianie pędu. Zmiana pędu tu, to iloczyn masy i zmiany prędkości, więc jeśli podzielimy impuls przez masę, otrzymamy zmianę prędkości. Możemy powiązać prędkości przed i po zderzeniu równaniem
| va2 = va1 + j n / ma | (7) |
| vb2 = vb1 − j n / mb | (8) |
Zmiana momentu pędu ciała A równa jest popędowi kątowemu danemu przez rap × j n . Następnie dzielimy przez moment bezwładności, aby przekształcić zmianę momentu pędu na zmianę prędkości kątowej i w efekcie wyznaczamy prędkości kątowe po zderzeniu
| ωa2 = ωa1 + (rap × j n) / Ia | (9) |
| ωb2 = ωb1 − (rbp × j n) / Ib | (10) |
Wyznaczanie wartości impulsu (popędu)
Teraz możemy połączyć wszystkie te równania i wyznaczyć wielkość impulsu j . Jeśli nie interesują cię szczegóły rozwiązywania układu równań, po prostu przejdź do wyrażenia dla j .
Zaczynamy od równania (6), a następnie podstawiamy prędkości względne z równań (4-5).
vab2 · n = −e vab1 · n
(vap2 − vbp2) · n = −e vab1 · n
(va2 + ωa2 × rap − vb2 − ωb2 × rbp) · n =
−e vab1 · n
Rozwijamy lewą stronę, używając zależności z impulsami w równaniach (7-10).
((va1 + j n / ma) + (ωa1 + (rap × j n) / Ia) × rap − (vb1 − j n / mb) − (ωb1 − (rbp × j n) / Ib) × rbp) · n = −e vab1 · n
Zauważamy, że lewa strona zawiera wielkość vab1 · n zgodnie z równaniem (4), więc przenosimy to na prawą stronę.
(j n / ma + (rap × j n) × rap / Ia + j n / mb + (rbp × j n) ×rbp / Ib) · n = −(1 + e) vab1 · n
Zauważ, że przyjęliśmy, że n jest znormalizowany, więc n · n = 1 . Ponadto, aby uprościć różne iloczyny wektorowe, możemy skorzystać ze wzoru dotyczącego iloczynu mieszanego trójki wektorów
(A × B) · C = (B × C) · A
i uzyskać następującą tożsamość
(A × B) × A · B = (A × B) · (A × B) = (A × B)2
(Kwadrat wektora oznacza tu iloczyn skalarny wektora przez siebie.) Następnie możemy to uprościć do
j (1 / ma + 1 / mb + (rap × n)2 / Ia + (rbp × n)2 / Ib) = −(1 + e) vab1 · n
Podzielenie obu stron przez wyrażenie w nawiasie po lewej, prowadzi do ostatecznej postaci naszego wzoru na j .
| (11) |
Za pomocą równania (11) możemy teraz obliczyć j w chwili zderzenia, a zatem, za pomocą wcześniejszych równań (7-10), obliczyć także prędkości po zderzeniu.
Możemy użyć tego samego wyrażenia do obliczenia kolizji ze ścianą, zakładając, że masa ściany jest nieskończona. Więc niech mb → ∞ i Ib → ∞ , a równanie (11) przyjmie postać
| j = | −(1 + e) vap1 · n |
| 1⁄ma + (rap × n)2 ⁄ Ia |
Wiele punktów kolizyjnych
Powyższa analiza obejmuje tylko przypadek pojedynczego uderzenia w narożnik i krawędź. Istnieje kilka innych jednoczesnych przypadków wielokrotnego oddziaływania, takich jak:
- Dwa wierzchołki obiektu A uderzają w pojedynczą ścianę
- Dwa wierzchołki obiektu A uderzają w obiekt B
- Dwa wierzchołki obiektu A uderzają w różne ściany
- Dwa wierzchołki obiektu A uderzają w różne obiekty
Jeśli występują jednoczesne uderzenia między niepowiązanymi obiektami, można je łatwo obsłużyć osobno. Załóżmy na przykład, że obiekty A i B zderzają się w tym samym czasie, co obiekty C i D, wówczas możemy poradzić sobie z każdą kolizją osobno, ponieważ nie wpływają one na siebie.
W przypadku dwóch sąsiadujących narożników obiektu A, uderzających w pojedynczą ścianę lub krawędź innego obiektu, zmieniamy punkt uderzenia na punkt środkowy między dwoma narożnikami, a następnie traktujemy go jak w innych kolizjach.
Bardziej skomplikowane przypadki, z narożnikami obiektu A uderzającymi w różne ściany lub kilka obiektów, nie są obsługiwane w tej symulacji. Kod obsługuje osobno każde oddziaływanie, co prawdopodobnie będzie błędne, ponieważ kolizje te nie są niezależne.
Zobacz Metody obsługi kolizji (en) gdzie omówiono zalety i wady różnych metod.
Kolizja spoczynkowa
Jeśli pobawisz się pokazaną powyżej symulacją, zauważysz, że łatwo "zawiesza się", co oznacza, że obiekty nakładają się na siebie i symulacja nie wie, jak kontynuować. Przy współczynniku restytucji < 1 jeśli popchniesz dwa obiekty do siebie siłą sprężyny myszy, symulacja zostanie zablokowana.
Symulacja blokuje się również, gdy przyspieszenie grawitacyjne > 0 i współczynnik restytucji < 1 . Problem występuje, gdy obiekt osiada na podłodze. Prędkość obiektu maleje z każdym zderzeniem, ponieważ współczynnik restytucji jest mniejszy niż jeden. W końcu prędkość staje się tak mała, że nie jest w stanie powstrzymać grawitacji przed wciągnięciem obiektu w podłogę. To powoduje zablokowanie symulacji.
Właściwą rzeczą do zrobienia w tym momencie (czego nie robi powyższa symulacja) jest rozpoznanie, że obiekt znajduje się w kontakcie spoczynkowym z podłogą i dodanie siły kontaktowej między przedmiotem a podłogą. Siła kontaktowa jest obliczana tak, żeby zapobiec zapadaniu się przedmiotu w podłogę. Zobacz symulację Bryła sztywna - siły kontaktowe, w której opisano jak to zrobić.
Większość symulacji myphysicslab "opartych na silniku fizyki" wykorzystuje ContactSim, klasę, która oprócz obliczeń impulsu kolizji opisanych powyżej, implementuje obliczenia kontaktu spoczynkowego.
Jednostki miary
Symulacje myPhysicsLab nie mają określonych jednostek miary, takich jak metry, kilogramy, sekundy. Jednostki są bezwymiarowe, mogą być interpretowane, jak chcesz, ale muszą być spójne w symulacji.
Na przykład, jeśli traktujemy jednostkę odległości jako jeden metr i jednostkę czasu jako jedną sekundę, to jednostka prędkości musi wynosić jeden metr/sekundę.
Dostosuj i udostępnij
Istnieje kilka sposobów na odtworzenie określonej konfiguracji eksperymentalnej. Najłatwiej jest kliknąć przycisk „udostępnij”.
- Zmodyfikuj symulację, zmieniając parametry, takie jak grawitacja, tłumienie oraz przeciągając obiekty za pomocą myszy.
- Kliknij przycisk „udostępnij”. Skopiuj adres URL z okna dialogowego.
- Udostępnij adres URL lub zapisz go w pliku tekstowym do późniejszego wykorzystania.
Gdy odbiorca kliknie adres URL, EasyScript osadzony w tym adresie powieli warunki, które zostały ustawione.
Zobacz Dostosowywanie symulacji myPhysicsLab (en) jak dodatkowo programować symulacje z bezpośrednim wykorzystaniem JavaScript lub EasyScript.
Opublikowano po raz pierwszy w lutym 2003 roku.