Co mówi twierdzenie Pitagorasa i jak je udowodnić?

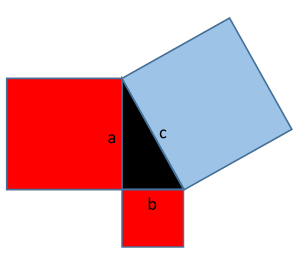
Twierdzenie Pitagorasa stwierdza, że w trójkącie prostokątnym o bokach długości a, b, c, pole kwadratu zbudowanego na najdłuższym boku (tu jest nim bok o długości c): c² jest równe sumie pól kwadratów zbudowanych na pozostałych dwóch bokach: a²+b².

Tu naprawdę chodzi o pola powierzchni: Pitagoras twierdzi, że na rysunku tutaj, pole powierzchni niebieskiego kwadratu, c×c=c², jest dokładnie równe sumie pól powierzchni dwóch czerwonych kwadratów, a²+b².

 

Nasz sposób na udowodnienie tego jest następujący: układamy cztery kopie naszego trójkąta o bokach a, b, c wokół kwadratu o boku c, jak na poniższym rysunku. Powstały duży kwadrat (czerwona linia) ma pole powierzchni równe czterokrotności pola powierzchni wyjściowego trójkąta plus pole powierzchni c² mniejszego kwadratu.

Teraz możemy przesuwać te trójkąty wewnątrz dużego kwadratu tak, żeby zobaczyć, że duży kwadrat składa się z tych czterech trójkątów oraz dwóch kwadratów, jeden o boku a, drugi b. Stąd wynika twierdzenie Pitagorasa.

Odkryj to samodzielnie! (dotknij/kliknij i przeciągnij trójkąty)

Wynik nie zależy od długości boków, byleby trójkąt był prostokątny. Wypróbuj różne długości boków.

Oczywiście możliwy też jest dowód algebraiczny, z porównania pól powierzchni: (a+b)²=c²+4×½×a×b