Obwód koła możemy przybliżyć z nadmiarem, podając obwód wielokąta foremnego opisanego na nim lub z niedomiarem, podając obwód wielokąta foremnego wpisanego.
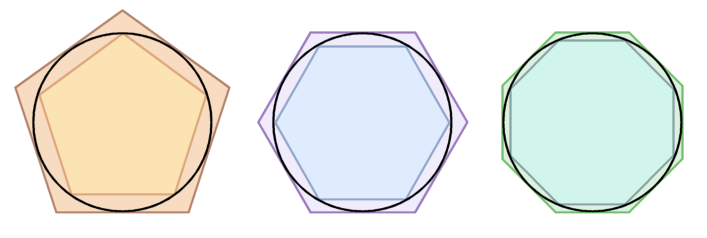
Symulacja demonstruje obliczenia obwodu koła jednostkowego za pomocą algorytmu podanego przez Archimedesa (287 − 212 p.n.e.). Bierzemy dwa wielokąty foremne - wpisany w okrąg i opisany na okręgu. Obwody wielokątów mogą być obliczone na podstawie twierdzenia Pitagorasa o trójkątach prostokątnych. Archimedesowi udało się wyznaczyć długości boków dwóch 96-kątów foremnych (dla 192-kątów już nie dał rady).
Ta symulacja zaczyna od kwadratów (liczba porządkowa n = 2, wierzchołki N = 2n = 4). Suwak zwiększa liczbę porządkową w krokach o 1, od n = 2 do n = 12 .
Rysunek po prawej stronie pokazuje podstawową konstrukcję pierwszego kroku aproksymacji od kwadratu do ośmiokąta. Wykorzystując ten rysunek, łatwo jest wyprowadzić wzór na długość boku wielokąta foremnego wpisanego o podwojonej liczbie wierzchołków (przy wielokącie opisanym postępujemy analogicznie).
Wraz ze wzrostem liczby wierzchołków oba wielokąty zbliżają się do okręgu dość szybko, a więc także i do siebie nawzajem. Już 32-kąty są trudne do rozróżnienia wizualnie.
Przycisk Resetuj przywraca n = 2.
W górnej części okna trzy pola liczbowe pokazują obwody wielokąta wpisanego (niebieski), wartość (2π) koła jednostkowego (czarny) i wielokąta opisanego (czerwony). Dla n = 12 (N = 4096) różnią się one na 6 miejscu po przecinku.